题目内容
等差数列8，5，2，…的第20项是（ ）
| A、68 | B、65 |
| C、-46 | D、-49 |
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：利用等差数列的通项公式求解．
解答：
解：等差数列8，5，2，…中，
a1=8，d=-3，
∴a20=8+19×（-3）
=-49．
故选：D．
a1=8，d=-3，
∴a20=8+19×（-3）
=-49．
故选：D．
点评：本题考查数列的第20项的求法，是基础题，解题时要认真审题，注意等差数列的第20项的求法．
练习册系列答案
相关题目
已知i为虚数单位，则复平面内表示复数z=i（1-i）的点在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
用反证法证明命题“设x，y∈（0，1），求证：对于a，b∈R，必存在满足条件的x，y，使|xy-ax-by|≥
成立．”第一步的假设为（ ）
| 1 |
| 3 |
A、对任意x，y∈（0，1），|xy-ax-by|≥
| ||
B、对任意x，y∈（0，1），|xy-ax-by|＜
| ||
C、存在x，y∈（0，1），使|xy-ax-by|＜
| ||
D、存在x，y∉（0，1），使|xy-ax-by|≥
|
过点P（a，5）作圆（x+2）2+（y-1）2=4的切线，切线长为2
，则a等于（ ）
| 3 |
| A、-1 | B、-2 | C、-3 | D、0 |
log
sin
π+log
cos
π的值是（ ）
| 2 |
| 5 |
| 12 |
| 2 |
| 5 |
| 12 |
| A、4 | B、1 | C、-4 | D、-1 |
从5名同学中选3人参加某项会议，则选法种数为（ ）
| A、15 | B、10 | C、20 | D、60 |
甲船在早6点至12点之间的任意时刻出发，则它早于8点出发的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
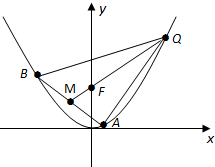已知抛物线C：x2=2py，的焦点为F，△ABQ的三个顶点都在抛物线C上，点M为AB的中点，
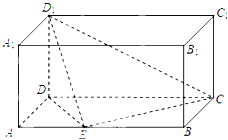在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，点E是棱AB上一点，且不为中点．