题目内容
若正数x,y满足x+4y-xy=0,则x+2y的最小值为 .
考点:基本不等式
专题:函数的性质及应用
分析:正数x,y满足x+4y-xy=0,可得y=
>0,(x>4).因此x+2y=x+
=x-4+
+6,利用基本不等式的性质即可得出.
| x |
| x-4 |
| 2x |
| x-4 |
| 8 |
| x-4 |
解答:
解:∵正数x,y满足x+4y-xy=0,
∴y=
>0,解得x>4.
∴x+2y=x+
=x-4+
+6≥2
+6=4
+6,当且仅当x=4+2
,y=
+1时取等号.
∴x+2y的最小值为6+4
,
故答案为:6+4
.
∴y=
| x |
| x-4 |
∴x+2y=x+
| 2x |
| x-4 |
| 8 |
| x-4 |
(x-4)•
|
| 2 |
| 2 |
| 2 |
∴x+2y的最小值为6+4
| 2 |
故答案为:6+4
| 2 |
点评:本题考查了基本不等式的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
sin(2π-α)cos(
| ||||
tan(α-3π)sin(
|
| A、-cosα | B、cosα |
| C、sinα | D、-sinα |
在圆x2+y2-2x-6y=0内,过点E(0,1)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为( )
A、5
| ||
B、20
| ||
C、15
| ||
D、10
|
“x=kπ+
(k∈Z)“是“tanx=1”成立的( )
| π |
| 4 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
 第三赛季甲、乙两名运动员每场比赛得分的茎叶图如图所示,则下列说法中正确的是( )
第三赛季甲、乙两名运动员每场比赛得分的茎叶图如图所示,则下列说法中正确的是( )| A、甲、乙两人单场得分的最高分都是9分 |
| B、甲、乙两人单场得分的中位数相同 |
| C、甲运动员的得分更集中,发挥更稳定 |
| D、乙运动员的得分更集中,发挥更稳定. |
已知锐角α的终边上一点P(sin40°,1+cos40°),则α等于( )
| A、10° | B、20° |
| C、70° | D、80° |
已知实数x,y满足
,若(-1,0)是使mx+y取得最大值的可行解,则实数m的取值范围是( )
|
| A、m≤3 | ||
| B、m≤-3 | ||
C、m≥-
| ||
D、m≥
|
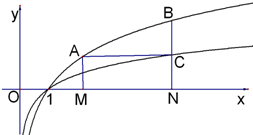 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx,(m>c>1)的图象交于点C,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx,(m>c>1)的图象交于点C,且AC与x轴平行.