题目内容
2.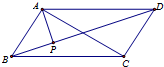 如图,在平行四边形ABCD中,AP⊥BD,垂足为P,且AP=2,则$\overrightarrow{AP}$•$\overrightarrow{AC}$=8.
如图,在平行四边形ABCD中,AP⊥BD,垂足为P,且AP=2,则$\overrightarrow{AP}$•$\overrightarrow{AC}$=8.
分析 设对角线AC、BD相交于O点,根据平行四边形的性质与向量加法法则,得到$\overrightarrow{AC}=2\overrightarrow{AO}$=2($\overrightarrow{AP}+\overrightarrow{PO}$),代入$\overrightarrow{AP}$•$\overrightarrow{AC}$,展开后即可求得答案.
解答 解:如图,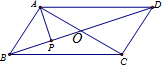
设对角线AC、BD相交于O点,
∵四边形ABCD是平行四边形,
∴$\overrightarrow{AC}=2\overrightarrow{AO}$=2($\overrightarrow{AP}+\overrightarrow{PO}$),
因此,$\overrightarrow{AP}•\overrightarrow{AC}$=$\overrightarrow{AP}•2\overrightarrow{AO}$=2$\overrightarrow{AP}•\overrightarrow{AO}$=2$\overrightarrow{AP}•(\overrightarrow{AP}+\overrightarrow{PO})$=2${\overrightarrow{AP}}^{2}+2\overrightarrow{AP}•\overrightarrow{PO}$,
∵|$\overrightarrow{AP}$|=2,$\overrightarrow{AP}⊥\overrightarrow{PO}$,
∴$|\overrightarrow{AP}{|}^{2}=4,\overrightarrow{AP}•\overrightarrow{PO}=0$,
由此可得$\overrightarrow{AP}•\overrightarrow{AC}=8$.
故答案为:8.
点评 本题在平行四边形中求向量的数量积,着重考查了平行四边形的性质、向量的线性运算性质、向量的数量积及其运算性质等知识,属于中档题.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案| 运动时间 性别 | 运动达人 | 非运动达人 | 合计 |
| 男 | 36 | ||
| 女 | 26 | ||
| 合计 | 100 |
(Ⅱ)将此样本的频率估计为总体的概率,随机调查该单位的3名男职工,设调查的3人中运动达人的人数为随机变量X,求X的分布列和数学期望E(X)及方差D(X).
附表及公式:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
| A. | (0,+∞) | B. | (1,+∞) | C. | (-1,+∞) | D. | R |
| A. | (2,$\frac{π}{3}$) | B. | (2,$\frac{π}{2}$) | C. | (2,$\frac{4π}{3}$) | D. | (2,$\frac{7π}{6}$) |
| A. | 2f(2)>3f(3) | B. | 2f(2)<3f(3) | C. | 2f(2)=3f(3) | D. | 无法确定 |
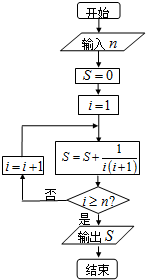
| A. | $\frac{100}{101}$ | B. | $\frac{99}{100}$ | C. | $\frac{98}{99}$ | D. | $\frac{97}{98}$ |