题目内容
7.已知函数f(x)=$\left\{{\begin{array}{l}{\frac{1}{2}\sqrt{{x^2}+1},x≥0}\\{-ln(1-x),x<0}\end{array}}$,若函数F(x)=f(x)-kx有且只有两个零点,则k的取值范围为($\frac{1}{2}$,1).分析 求出双曲线的渐近线方程,y=-ln(1-x)在x=0处的切线方程,通过图象观察,即可得出结论.
解答 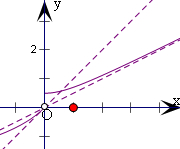 解:由题意,x≥0,f(x)=$\frac{1}{2}$$\sqrt{1+{x}^{2}}$,
解:由题意,x≥0,f(x)=$\frac{1}{2}$$\sqrt{1+{x}^{2}}$,
为双曲线4y2-x2=1在第一象限的部分,
渐近线方程为y=$\frac{1}{2}$x;
由y=-ln(1-x),
可得y′=$\frac{1}{1-x}$=1,可得x=0,
即y=-ln(1-x)在x=0处的切线方程为y=x,
此时函数F(x)=f(x)-kx有且只有1个零点,
若函数F(x)=f(x)-kx有且只有两个零点,
则k的取值范围为($\frac{1}{2}$,1),
故答案为:($\frac{1}{2}$,1).
点评 本题考查函数的零点,考查导数知识的运用,考查学生分析解决问题的能力,以及数形结合的思想方法,知识综合性强.

练习册系列答案
相关题目
17.已知函数f(x)=-x3+ax2+bx+c的一个极值点是x=1,则9a+3b的最小值是( )
| A. | 10 | B. | $2\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | $4\sqrt{6}$ |
18.如图所示的程序框图中的错误是( )
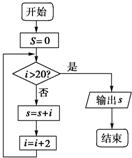

| A. | i没有赋值 | B. | 循环结构有错 | C. | s的计算不对 | D. | 判断条件不成立 |
2.已知定义域为(0,+∞)的函数f(x)满足:(1)对任意x∈(0,+∞),恒有f(2x)=2f(x)成立;(2)当x∈(1,2]时,f(x)=2-x.
给出如下结论:
①对任意m∈Z,有f(2m)=0;
②函数f(x)的值域为[0,+∞);
③存在n∈Z,使得f(2n+1)=9;
正确的有( )
给出如下结论:
①对任意m∈Z,有f(2m)=0;
②函数f(x)的值域为[0,+∞);
③存在n∈Z,使得f(2n+1)=9;
正确的有( )
| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
12.某单位有男职工600名,女职工400人,在单位想了解本单位职工的运动状态,根据性别采取分层抽样的方法从全体职工中抽取100人,调查他们平均每天运动的时间(单位:小时),统计表明该单位职工平均每天运动的时间范围是[0,2].若规定平均每天运动的时间不少于1小时的为“运动达人”,低于1小时的为“非运动达人”.根据调查的数据,按性别与是否为运动达人进行统计,得到如下2×2列联表.
(Ⅰ)请根据题目信息,将2×2列联表中的数据补充完整,并通过计算判断能否在犯错误概率不超过0.025的前提下认为性别与是否为运动达人有关;
(Ⅱ)将此样本的频率估计为总体的概率,随机调查该单位的3名男职工,设调查的3人中运动达人的人数为随机变量X,求X的分布列和数学期望E(X)及方差D(X).
附表及公式:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 运动时间 性别 | 运动达人 | 非运动达人 | 合计 |
| 男 | 36 | ||
| 女 | 26 | ||
| 合计 | 100 |
(Ⅱ)将此样本的频率估计为总体的概率,随机调查该单位的3名男职工,设调查的3人中运动达人的人数为随机变量X,求X的分布列和数学期望E(X)及方差D(X).
附表及公式:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
19.已知向量$\overrightarrow{a}$=(2cosφ,2sinφ),φ∈(90°,180°),$\overrightarrow{b}$=(1,1),则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | φ | B. | 45°+φ | C. | 135°-φ | D. | φ-45° |
17.定义在(0,+∞)上的可导函数f(x)满足:当x∈(0,e)时f(x)+xf′(x)>$\frac{1}{e}$当x∈(e,+∞)时f(x)+xf′(x)<$\frac{1}{e}$则下列对于2f(2),3f(3)大小关系的结论成立的是( )
| A. | 2f(2)>3f(3) | B. | 2f(2)<3f(3) | C. | 2f(2)=3f(3) | D. | 无法确定 |