题目内容
已知经过同一点的n(n∈N*,n≥3)个平面,任意三个平面不经过同一条直线.若这n个平面将空间分成f(n)个部分,则f(n)=( )
A、
| ||
B、
| ||
| C、n2-n+1 | ||
| D、n2-n+2 |
考点:归纳推理
专题:规律型
分析:两个平面把空间分成4个部分,增加一平面,与前两个平面不过同一直线,则第三个平面与前两个平面有两条交线,两条交线把第三个平面分成两个部分,每一部分将其所在的空间一分为二,则三个平面把空间分成8个部分,即f(3)=8=32-3+2;由此结论可得过同一点且不经过同一直线的n个平面把空间分成n2-n+2个部分.
解答:
解:∵一个平面把空间分成两个部分,
即f(1)=1=12-1+2;
∵两个相交平面把空间分成四个部分,
即f(2)=4=22-2+2;
若第三个平面和前两相交平面经过同一点,且三个平面不过同一直线,则第三个平面与前两个平面的交线相交,这样能把空间分成8个部分,
即f(3)=8=32-3+2;
…
有n个面时,再添加1个面,与其它的n个面有n条交线,n条交线将此平面分成2n个部分,
每一部分将其所在空间一分为二,
则 f(n+1)=f(n)+2n.
利用叠加法,
则 f(n)-f(1)=[2+4+6+…+2(n-1)]
=
=n2-n
∴f(n)=n2-n+2.
故选:D
即f(1)=1=12-1+2;
∵两个相交平面把空间分成四个部分,
即f(2)=4=22-2+2;
若第三个平面和前两相交平面经过同一点,且三个平面不过同一直线,则第三个平面与前两个平面的交线相交,这样能把空间分成8个部分,
即f(3)=8=32-3+2;
…
有n个面时,再添加1个面,与其它的n个面有n条交线,n条交线将此平面分成2n个部分,
每一部分将其所在空间一分为二,
则 f(n+1)=f(n)+2n.
利用叠加法,
则 f(n)-f(1)=[2+4+6+…+2(n-1)]
=
| [2+2(n-1)](n-1) |
| 2 |
∴f(n)=n2-n+2.
故选:D
点评:本题考查了类比推理,类比推理是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,此题是基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
数列
,-
,
,-
…的一个通项公式是( )
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 8 |
| 7 |
| 16 |
A、an=(-1)n•
| ||
B、an=(-1)n+1•
| ||
C、an=(-1)n•
| ||
D、an=(-1)n+1•
|
如图,在正方体ABCD-A1B1C1D1中,异面直线A1D与D1C所成的角为( )


| A、30° | B、45° |
| C、60° | D、90° |
若a>b,则下列不等式成立的是( )
A、
| ||||||
| B、a>|b| | ||||||
C、
| ||||||
| D、lna>lnb |
等比数列前n项和为Sn有人算得S1=8,S2=20,S3=36,S4=65,后来发现有一个数算错了,错误的是( )
| A、S1 |
| B、S2 |
| C、S3 |
| D、S4 |
在等差数列{an}中,已知a3+a8=9,则3a5+a7=( )
| A、10 | B、18 | C、20 | D、28 |
某学校从1208名学生中抽取20人参加义务劳动,规定采用下列方式选取:先用简单随机抽样的方法从1208人中剔除8人,剩下的1200人再按系统抽样的方法抽取,那么在1208人中每个人入选的概率为( )
A、都相等且等于
| ||
B、都相等且等于
| ||
| C、不全相等 | ||
| D、均不相等 |
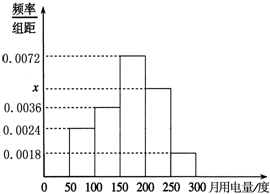 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到300度之间,频率分布直方图所示,则在这些用户中,用电量落在区间[150,250)内的户数为( )
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到300度之间,频率分布直方图所示,则在这些用户中,用电量落在区间[150,250)内的户数为( )