题目内容
已知数列{an}满足:a1=
,an+1=sin(
an),n∈N*
(Ⅰ)求证:0<an<an+1<1;
(Ⅱ)求证:sin[
(1-an)]<
;
(Ⅲ)求证:an≥1-
(
)n-1.
| 1 |
| 2 |
| π |
| 2 |
(Ⅰ)求证:0<an<an+1<1;
(Ⅱ)求证:sin[
| π |
| 4 |
| 1 |
| 2 |
(Ⅲ)求证:an≥1-
| 1 |
| 2 |
| π |
| 4 |
考点:数列与不等式的综合,数列与三角函数的综合
专题:导数的综合应用
分析:(Ⅰ)首先利用数学归纳法证0<an<1,然后利用数学归纳法证明an<an+1;
(Ⅱ)由(Ⅰ)知
≤an<1,然后求出
(1-an)的范围,再利用正弦函数的单调性证明sin[
(1-an)]<
;
(Ⅲ)由1-an=1-sin(
an-1)=1-cos(
-
an-1)=2sin2[
(1-an-1)],结合(Ⅱ)可得2sin[
(1-an-1)]<1,再由x∈(0,
)时,sinx<x可得要证的结论.
(Ⅱ)由(Ⅰ)知
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
(Ⅲ)由1-an=1-sin(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
解答:
证明:(Ⅰ)先证0<an<1.
当n=1时,a1=
,满足0<a1<1;
假设当n=k时,0<ak<1,
当n=k+1时,∵0<
ak<
,∴0<sin(
ak)<1.
即0<ak+1<1.
再证:an<an+1.
当n=1时,a1=
,a2=sin(
a1)=sin
=
,∴a1<a2;
假设n=k时,0<ak<ak+1<1.
当n=k+1时,0<
ak<
ak+1<
,
∵f(x)=sinx在(0,
)上单调递增,
∴sin(
ak)<sin(
ak+1),即ak+1<ak+2.
∴n=k+1时,ak<ak+1.
综上,0<ak<ak+1<1;
(Ⅱ)由(Ⅰ)可知:
≤an<1.
∴0<1-an≤
.
∴0<
(1-an)≤
.
∴sin[
(1-an)]≤sin
<sin
=
.
即sin[
(1-an)]<
.
(Ⅲ)1-an=1-sin(
an-1)=1-cos(
-
an-1)=2sin2[
(1-an-1)].
由(Ⅱ)知:2sin[
(1-an-1)]<1.
∴2sin2[
(1-an-1)]<sin[
(1-an-1)].
又∵x∈(0,
)时,sinx<x,
∴sin[
(1-an-1)]<
(1-an-1).
即1-an<
(1-an-1)<(
)2(1-an-2)<…<(
)n-1(1-a1)=
(
)n-1.
∴an≥1-
(
)n-1.
当n=1时,a1=
| 1 |
| 2 |
假设当n=k时,0<ak<1,
当n=k+1时,∵0<
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
即0<ak+1<1.
再证:an<an+1.
当n=1时,a1=
| 1 |
| 2 |
| π |
| 2 |
| π |
| 4 |
| ||
| 2 |
假设n=k时,0<ak<ak+1<1.
当n=k+1时,0<
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∵f(x)=sinx在(0,
| π |
| 2 |
∴sin(
| π |
| 2 |
| π |
| 2 |
∴n=k+1时,ak<ak+1.
综上,0<ak<ak+1<1;
(Ⅱ)由(Ⅰ)可知:
| 1 |
| 2 |
∴0<1-an≤
| 1 |
| 2 |
∴0<
| π |
| 4 |
| π |
| 8 |
∴sin[
| π |
| 4 |
| π |
| 8 |
| π |
| 6 |
| 1 |
| 2 |
即sin[
| π |
| 4 |
| 1 |
| 2 |
(Ⅲ)1-an=1-sin(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
由(Ⅱ)知:2sin[
| π |
| 4 |
∴2sin2[
| π |
| 4 |
| π |
| 4 |
又∵x∈(0,
| π |
| 2 |
∴sin[
| π |
| 4 |
| π |
| 4 |
即1-an<
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
∴an≥1-
| 1 |
| 2 |
| π |
| 4 |
点评:本题是数列与三角函数的综合题,考查了利用数学归纳法证明数列不等式,考查了数列的函数特性,训练了同角三角函数的基本关系式的应用,属有一定难度题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
| 3 | a |
| 3 | b |
| 3 | a-b |
| A、ab(b-a)>0 |
| B、ab>0且a>b |
| C、ab<0且a<b |
| D、ab(b-a)<0 |
设a>b>0,a+b=1且x=ba,y=ab,z=log
a则x,y,z之间的大小关系是( )
| 1 |
| b |
| A、y<x<z |
| B、y<z<x |
| C、z<y<x |
| D、z<x<y |
已知过定点P(2,0)的直线l与曲线y=
相交于A,B两点,O为坐标原点,当S△AOB=1时,直线l的倾斜角为( )
| 2-x2 |
| A、150° | B、135° |
| C、120° | D、不存在 |
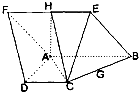 如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H,G分别是线段EF,BC的中点.
如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H,G分别是线段EF,BC的中点.
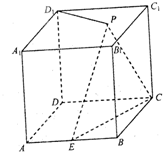 在棱长为2的正方体ABCD-A1B1C1D1中,E为棱AB的中点,点P在平面A1B1C1D1内,若D1P⊥平面PCE,试求线段D1P的长.
在棱长为2的正方体ABCD-A1B1C1D1中,E为棱AB的中点,点P在平面A1B1C1D1内,若D1P⊥平面PCE,试求线段D1P的长.