题目内容
已知函数f(x)=x2+a(x+lnx),x>0,a∈R是常数.
(1)求函数y=f(x)的图象在点(1,f(1))处的切线方程;
(2)若函数y=f(x)图象上的点都在第一象限,试求常数a的取值范围;
(3)证明:?a∈R,存在ξ∈(1,e),使f′(ξ)=
.
(1)求函数y=f(x)的图象在点(1,f(1))处的切线方程;
(2)若函数y=f(x)图象上的点都在第一象限,试求常数a的取值范围;
(3)证明:?a∈R,存在ξ∈(1,e),使f′(ξ)=
| f(e)-f(1) |
| e-1 |
考点:利用导数研究曲线上某点切线方程,导数在最大值、最小值问题中的应用
专题:计算题,证明题,分类讨论,导数的综合应用
分析:(1)求出函数f(x)的导数,求出切线的斜率和切点,由点斜式方程即可得到切线方程;
(2)讨论a=0,a>0,a<0,运用对数函数的性质,以及分离参数,构造函数应用导数求极值、最值,即可得到a的范围;
(3)设函数g(x)=f′(x)-
=2x-(e+1)+
-
,计算g(1),g(e),讨论当a>e(e-1)2或a<
时,由零点存在定理,即可得证;当
≤a≤e(e-1)2时,求出g(x)的最小值,判断它小于0,再由零点存在定理,即可得证.
(2)讨论a=0,a>0,a<0,运用对数函数的性质,以及分离参数,构造函数应用导数求极值、最值,即可得到a的范围;
(3)设函数g(x)=f′(x)-
| f(e)-f(1) |
| e-1 |
| a |
| x |
| a |
| e-1 |
| (e-1)2 |
| e-2 |
| (e-1)2 |
| e-2 |
解答:
(1)解:函数f(x)=x2+a(x+lnx)的导数f′(x)=2x+a(1+
),
f(1)=1+a,f′(1)=2+2a,
则函数y=f(x)的图象在点(1,f(1))处的切线为y-(1+a)=(2+2a)(x-1),
即y=(1+a)(2x-1);
(2)解:①a=0时,f(x)=x2,因为x>0,所以点(x,x2)在第一象限,
依题意,f(x)=x2+a(x+lnx)>0;
②a>0时,由对数函数性质知,x∈(0,1)时,lnx∈(-∞,0),alnx∈(-∞,0),
从而“?x>0,f(x)=x2+a(x+lnx)>0”不成立;
③a<0时,由f(x)=x2+a(x+lnx)>0得
<-(
+
lnx),
设g(x)=-(
+
lnx),g′(x)=
+
,
则g(x)≥g(1)=-1,从而
<-(
+
lnx)<-1,-1<a<0;
综上所述,常数a的取值范围-1<a≤0.
(3)证明:直接计算知
=e+1+a+
,
设函数g(x)=f′(x)-
=2x-(e+1)+
-
,
g(1)=1-e+a-
=
,g(e)=e-1+
-
=
,
当a>e(e-1)2或a<
时,g(1)g(e)=-
<0,
因为y=g(x)的图象是一条连续不断的曲线,所以存在ξ∈(1,e),使g(ξ)=0,
即ξ∈(1,e),使f′(ξ)=
;
当
≤a≤e(e-1)2时,g(1)、g(e)≥0,而且g(1)、g(e)之中至少一个为正,
由均值不等式知,g(x)≥2
-
,等号当且仅当x=
∈(1,e)时成立,
所以g(x)有最小值m=2
-
=
,且m=
=
<0,
此时存在ξ∈(1,e)(ξ∈(1,
)或ξ∈(
,e)),使g(ξ)=0.
综上所述,?a∈R,存在ξ∈(1,e),使f′(ξ)=
.
| 1 |
| x |
f(1)=1+a,f′(1)=2+2a,
则函数y=f(x)的图象在点(1,f(1))处的切线为y-(1+a)=(2+2a)(x-1),
即y=(1+a)(2x-1);
(2)解:①a=0时,f(x)=x2,因为x>0,所以点(x,x2)在第一象限,
依题意,f(x)=x2+a(x+lnx)>0;
②a>0时,由对数函数性质知,x∈(0,1)时,lnx∈(-∞,0),alnx∈(-∞,0),
从而“?x>0,f(x)=x2+a(x+lnx)>0”不成立;
③a<0时,由f(x)=x2+a(x+lnx)>0得
| 1 |
| a |
| 1 |
| x |
| 1 |
| x2 |
设g(x)=-(
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x3 |
| 2lnx |
| x3 |
| x | (0,1) | 1 | (1,+∞) |
| g′(x) | - | 0 | + |
| g(x) | ↘ | 极小值 | ↗ |
| 1 |
| a |
| 1 |
| x |
| 1 |
| x2 |
综上所述,常数a的取值范围-1<a≤0.
(3)证明:直接计算知
| f(e)-f(1) |
| e-1 |
| a |
| e-1 |
设函数g(x)=f′(x)-
| f(e)-f(1) |
| e-1 |
| a |
| x |
| a |
| e-1 |
g(1)=1-e+a-
| a |
| e-1 |
| a(e-2)-(e-1)2 |
| e-1 |
| a |
| e |
| a |
| e-1 |
| e(e-1)2-a |
| e(e-1) |
当a>e(e-1)2或a<
| (e-1)2 |
| e-2 |
| [a(e-2)-(e-1)2][a-e(e-1)2] |
| e(e-1)2 |
因为y=g(x)的图象是一条连续不断的曲线,所以存在ξ∈(1,e),使g(ξ)=0,
即ξ∈(1,e),使f′(ξ)=
| f(e)-f(1) |
| e-1 |
当
| (e-1)2 |
| e-2 |
由均值不等式知,g(x)≥2
| 2a |
| a+e2-1 |
| e-1 |
|
所以g(x)有最小值m=2
| 2a |
| a+e2-1 |
| e-1 |
-a+2(e-1)
| ||
| e-1 |
-a+2(e-1)
| ||
| e-1 |
-[
| ||||
| e-1 |
此时存在ξ∈(1,e)(ξ∈(1,
|
|
综上所述,?a∈R,存在ξ∈(1,e),使f′(ξ)=
| f(e)-f(1) |
| e-1 |
点评:本题考查导数的综合应用:求切线方程和求单调区间、极值和最值,同时考查函数的零点存在定理,以及分类讨论的思想方法,属于综合题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
定义在[-2,2]上的偶函数f(x)在区间[0,2]上单调递减,若f(1-m)<f(m),则实数m的取值范围是( )
A、m<
| ||
B、m>
| ||
C、-1≤m<
| ||
D、
|
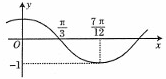 函数f(x)=sin(ωx+φ)({其中ω>0,|φ|<
函数f(x)=sin(ωx+φ)({其中ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
某商场经营的某种包装的大米质量服从正态分布N(10,0.12)(单位:kg),任选一袋这种大米,则质量在9.810.2kg的概率是( )
| A、0.9544 |
| B、0.9744 |
| C、0.6826 |
| D、0.5 |
已知直线ax-by-2=0与曲线f(x)=x3在点P(1,f(1))处的切线互相垂直,则
=( )
| a |
| b |
A、
| ||
B、
| ||
C、-
| ||
D、-
|