题目内容
设集合M={(x,y)|y=x+b},N={(x,y)|y=3-
},当M∩N≠∅时,则实数b的取值范围是 .
| 4x-x2 |
考点:交集及其运算
专题:集合
分析:由已知得直线y=x+b与圆(x-2)2+(y-3)2=4有交点,由此能求出实数b的取值范围.
解答:
解:∵集合M={(x,y)|y=x+b},N={(x,y)|y=3-
},
M∩N≠∅,
∴直线y=x+b与半圆(x-2)2+(y-3)2=4(1≤x≤3)有交点,
半圆(x-2)2+(y-3)2=4(1≤x≤3)表示:
圆心在(2,3),半径为 2 的圆的下半部分,
y=x+b表示斜率为1的平行线,
其中b是直线在y轴上的截距,
当直线与圆相切时,圆心到直线的距离等于半径,
即圆心(2,3)到直线y=x+b的距离d=
=2,
解得b=1-2
或b=1+2
(舍),
由图知b的取值范围是[1-2
,3].
∴实数b的取值范围是[1-2
,3].
故答案为:[1-2
,3].
| 4x-x2 |
M∩N≠∅,
∴直线y=x+b与半圆(x-2)2+(y-3)2=4(1≤x≤3)有交点,
半圆(x-2)2+(y-3)2=4(1≤x≤3)表示:

圆心在(2,3),半径为 2 的圆的下半部分,
y=x+b表示斜率为1的平行线,
其中b是直线在y轴上的截距,
当直线与圆相切时,圆心到直线的距离等于半径,
即圆心(2,3)到直线y=x+b的距离d=
| |2-3+b| | ||
|
解得b=1-2
| 2 |
| 2 |
由图知b的取值范围是[1-2
| 2 |
∴实数b的取值范围是[1-2
| 2 |
故答案为:[1-2
| 2 |
点评:本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
相关题目
下列式子成立的是( )
| A、0.52>1 |
| B、20.5>1 |
| C、log20.5>1 |
| D、log0.52>1 |
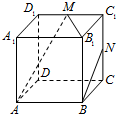 如图所示,在正方体ABCD A1B1C1D1中,M、N分别是棱C1D1,C1C的中点.给出以下四个结论:
如图所示,在正方体ABCD A1B1C1D1中,M、N分别是棱C1D1,C1C的中点.给出以下四个结论:
