题目内容
3.一个椭圆中心在原点,焦点F1,F2在x轴上,P(2,$\sqrt{3}$)是椭圆上一点,且|PF1|,|F1F2|,|PF2|成等差数列,则椭圆方程为$\frac{x^2}{8}+\frac{y^2}{6}=1$.分析 设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),由已知结合椭圆性质及等差数列性质列出方程求出a,b,由此能求出椭圆方程.
解答 解:∵个椭圆中心在原点,焦点F1,F2在x轴上,
∴设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),
∵P(2,$\sqrt{3}$)是椭圆上一点,且|PF1|,|F1F2|,|PF2|成等差数列,
∴$\left\{\begin{array}{l}{\frac{4}{{a}^{2}}+\frac{3}{{b}^{2}}=1}\\{2a=4c}\end{array}\right.$,且a2=b2+c2,
解得a=2$\sqrt{2}$,b=$\sqrt{6}$,c=$\sqrt{2}$,
∴椭圆方程为$\frac{x^2}{8}+\frac{y^2}{6}=1$.
故答案为:$\frac{x^2}{8}+\frac{y^2}{6}=1$.
点评 本题考是椭圆方程的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知集合A={y|y=2x},B={y|y=$\sqrt{x-1}$},则A∩B等于( )
| A. | {y|y≥0} | B. | {y|y>0} | C. | {y|y≥1} | D. | {y|y>1} |
13.设全集U=R,集合A={x|log2x≤2},$B=\left\{{x|\frac{4}{3-x}≥1}\right\}$,则A∩B=( )
| A. | [-1,3) | B. | (-∞,-1]∪(3,4] | C. | (0,3] | D. | (0,3) |
 如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,求异面直线AB1和BM所成的角的大小.(以B为坐标原点,BC为x轴,BB1为z轴,建立空间直角坐标系,利用空间向量求解)
如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,求异面直线AB1和BM所成的角的大小.(以B为坐标原点,BC为x轴,BB1为z轴,建立空间直角坐标系,利用空间向量求解)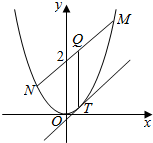 已知抛物线C:x${\;}^{2}=\frac{1}{2}y$,直线y=kx+2交C于M、N两点,Q是线段MN的中点,过Q作x轴的垂线交C于点T.
已知抛物线C:x${\;}^{2}=\frac{1}{2}y$,直线y=kx+2交C于M、N两点,Q是线段MN的中点,过Q作x轴的垂线交C于点T.