题目内容
一个几何体的三视图如图所示，则该几何体的体积为 ．
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：三视图中长对正，高对齐，宽相等；由三视图想象出直观图，一般需从俯视图构建直观图，该几何体为直四棱柱．
解答：
解：该几何体为直四棱柱，
底面为直角梯形，
S=
（4+5）×3=
；
h=4；
故V=Sh=
×4=54；
故答案为：54．
底面为直角梯形，
S=
| 1 |
| 2 |
| 27 |
| 2 |
h=4；
故V=Sh=
| 27 |
| 2 |
故答案为：54．
点评：三视图中长对正，高对齐，宽相等；由三视图想象出直观图，一般需从俯视图构建直观图，本题考查了学生的空间想象力，识图能力及计算能力．
练习册系列答案
相关题目
如图所示，在边长为2的正方形中有一封闭曲线围成的阴影区域．在正方形中随机撒一粒豆子，它落在阴影区域内的概率为如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的表面积是（ ）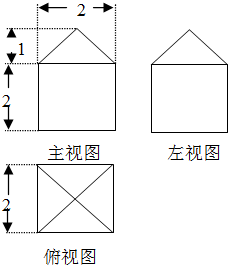
A、（20+4
| ||
| B、21 cm | ||
C、（24+4
| ||
| D、24 cm |
一个几何体的三视图如图所示，则这个几何体的表面积为（ ）
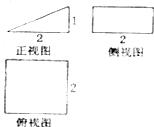
A、6+
| ||
B、6+2
| ||
C、8+
| ||
D、8+2
|
已知x、y的取值如表：从散点图分析，y与x线性相关，且回归方程为
=0.95x+a，则a=（ ）
 |
| y |
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A、2.6 | B、4 |
| C、4.5 | D、条件不足，无法求解 |