题目内容
空间四边形ABCD中AB⊥CD，AC⊥BD，则AD与BC所成角的大小为 ．
考点：异面直线及其所成的角
专题：空间位置关系与距离
分析：作AP垂直于平面BDC，P是垂足，连接CP，DP，BP，CP，DP，BP分别是AC，AD，AB在平面ABC内的射影，由AC⊥BD，AB⊥CD，知点P是△BDC的垂心．故DP垂直于BC．由三垂线定理，知AD⊥BC．
解答：
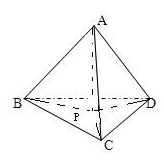解：作AP垂直于平面BDC，P是垂足，连接CP，DP，BP，
CP，DP，BP分别是AC，AD，AB在平面BCD内的射影，
∵AC⊥BD，
∴由三垂线定理的逆定理知BD⊥CP．
∵AB⊥CD，
∴由三垂线定理的逆定理知CD⊥BP
∴点P是△BDC的垂心．
∴DP垂直于BC．
由三垂线定理，知AD⊥BC．
故AD与BC所成角的大小为90°，
故答案为：90°
解：作AP垂直于平面BDC，P是垂足，连接CP，DP，BP，CP，DP，BP分别是AC，AD，AB在平面BCD内的射影，
∵AC⊥BD，
∴由三垂线定理的逆定理知BD⊥CP．
∵AB⊥CD，
∴由三垂线定理的逆定理知CD⊥BP
∴点P是△BDC的垂心．
∴DP垂直于BC．
由三垂线定理，知AD⊥BC．
故AD与BC所成角的大小为90°，
故答案为：90°
点评：本题考查空间中直线与直线之间的位置关系，是基础题．解题时要认真审题，仔细解答，注意三垂线定理及其逆定理的灵活运用．
练习册系列答案
名校课堂系列答案
相关题目
数列{an}满足an+1+（-1）nan=n，则{an}的前60项和等于（ ）
| A、960 | B、1920 |
| C、930 | D、1860 |
已知f（x）=
，则下列结论成立的是（ ）
|
| A、f（x）在x=0处连续 | ||
B、
| ||
C、
| ||
D、
|
设a，b，c表示三条不同直线，α，β表示两个不同平面，则下列命题中逆命题不成立的是（ ）
| A、b?β，c是α在β内的射影，若b⊥c，则b⊥a |
| B、b?α，c?α，若c∥α，则b∥c |
| C、c⊥α，若c⊥β，则α∥β |
| D、b?β，若b⊥α，则β⊥α |
如图所示，在边长为2的正方形中有一封闭曲线围成的阴影区域．在正方形中随机撒一粒豆子，它落在阴影区域内的概率为