题目内容
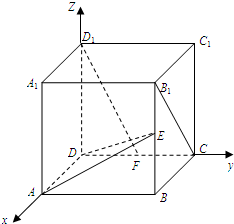 如图,在正方体ABCD-A1B1C1D1中,AB=2,E,F分别是BB1,CD的中点,(如图建立空间直角坐标系)
如图,在正方体ABCD-A1B1C1D1中,AB=2,E,F分别是BB1,CD的中点,(如图建立空间直角坐标系)(1)求证:D1F⊥平面ADE;
(2)求异面直线EF和CB1所成的角.
考点:直线与平面垂直的判定,异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)依题意分别求得A,E,D1和F的坐标取得)
和
,二者相乘等于0即可证明出AE⊥D1F进而根据线面垂直的性质证明出D1F⊥AD,最后根据线面垂直的判定定理证明出D1F⊥平面ADE.
(2)分别求得
和
,利用向量的夹角公式求得异面直线所成的角.
| AE |
| D1F |
(2)分别求得
| EF |
| CB1 |
解答:
(1)证明:依题意知D(0,0,0),A(2,0,0),F(0,1,0),E(2,2,1),A1(2,0,2),D1(0,0,2),
=(0,0,1),
=(0,1,-2),∴
•
=0,
∴AE⊥D1F;
∵AD⊥平面CDD1C1,D1F?平面CDD1C1,
∴D1F⊥AD,
∵AE?平面ADE,AD?平面ADE,AE∩AD=A,
∴D1F⊥平面ADE.
(2)解:依题意可知B1(1,1,1),C(0,1,0),F(0,1,0),E(2,2,1),
∴
=(2,1,1),
=(1,0,1),
∴cos<
,
)=
=
=
,
∴异面直线EF和CB1所成的角为30°.
| AE |
| D1F |
| AE |
| D1F |
∴AE⊥D1F;
∵AD⊥平面CDD1C1,D1F?平面CDD1C1,
∴D1F⊥AD,
∵AE?平面ADE,AD?平面ADE,AE∩AD=A,
∴D1F⊥平面ADE.
(2)解:依题意可知B1(1,1,1),C(0,1,0),F(0,1,0),E(2,2,1),
∴
| EF |
| CB1 |
∴cos<
| EF |
| CB1 |
| ||||
|
|
| 2+0+1 | ||||
|
| ||
| 2 |
∴异面直线EF和CB1所成的角为30°.
点评:本题主要考查了线面垂直和空间向量的应用.考查了学生综合分析和运算能力.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
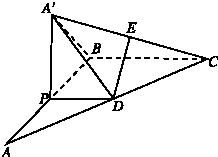 如图,在△ABC中,∠B=
如图,在△ABC中,∠B=