题目内容
第22届索契冬奥会期间，来自俄罗斯国际奥林匹克大学的男、女大学生共9名志愿者被随机地平均分配到速滑、冰壶、自由式滑雪这三个岗位服务，且速滑岗位至少有一名女大学生志愿者的概率是
（Ⅰ）求冰壶岗位至少有男、女大学生志愿者各一人的概率；
（Ⅱ）设随机变量X为在自由式滑雪岗位服务的男大学生志愿者的人数，求X的分布列及期望．
| 16 |
| 21 |
（Ⅰ）求冰壶岗位至少有男、女大学生志愿者各一人的概率；
（Ⅱ）设随机变量X为在自由式滑雪岗位服务的男大学生志愿者的人数，求X的分布列及期望．
考点：离散型随机变量的期望与方差,等可能事件的概率
专题：应用题,概率与统计
分析：（Ⅰ）先求出女大学生志愿者3人，男大学生志愿者6人，利用对立事件，即可求冰壶岗位至少有男、女大学生志愿者各一人的概率；
（Ⅱ）确定X的可能取值，求出相应的概率，即可求出X的分布列及期望．
（Ⅱ）确定X的可能取值，求出相应的概率，即可求出X的分布列及期望．
解答：
解：（Ⅰ）记速滑岗位至少有一名女大学生志愿者，为事件A，则A的对立事件为“速滑岗位没有一名女大学生志愿者”，设为x人（1≤x＜9），则P（A）=1-
=
，
∴（9-x）（8-x）（7-x）=120，∴x=3，
∴女大学生志愿者3人，男大学生志愿者6人，
记冰壶岗位至少有男、女大学生志愿者各一人为事件B，则P（B）=1-
=
；
（Ⅱ）X的可能取值为0，1，2，3，则
P（X=0）=
=
，P（X=1）=
=
，P（X=2）=
=
，P（X=3）=
=
，
∴X的分布列为
EX=0×
+1×
+2×
+3×
=2．
| ||
|
| 16 |
| 21 |
∴（9-x）（8-x）（7-x）=120，∴x=3，
∴女大学生志愿者3人，男大学生志愿者6人，
记冰壶岗位至少有男、女大学生志愿者各一人为事件B，则P（B）=1-
| ||||
|
| 3 |
| 4 |
（Ⅱ）X的可能取值为0，1，2，3，则
P（X=0）=
| ||
|
| 1 |
| 84 |
| ||||||
|
| 3 |
| 14 |
| ||||||
|
| 15 |
| 28 |
| ||||
|
| 5 |
| 21 |
∴X的分布列为
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 84 |
| 3 |
| 14 |
| 15 |
| 28 |
| 5 |
| 21 |
点评：本题主要考查古典概型及其概率计算公式的应用，考查分布列及数学期望，属于中档题．
练习册系列答案
相关题目
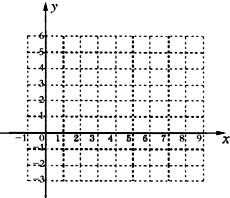设函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜
如图，斜三棱柱ABC-A1B1C1的所有棱长均为a，侧面B1C1CB⊥底面ABC，且AC1⊥BC．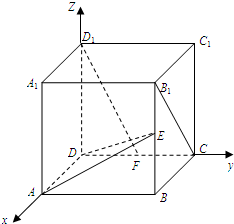
如图，在正方体ABCD-A1B1C1D1中，AB=2，E，F分别是BB1，CD的中点，（如图建立空间直角坐标系）