题目内容
16.若双曲线9y2-mx2=1的一个顶点到它的一条渐近线的距离为$\frac{1}{5}$,则m等于( )| A. | 25 | B. | 16 | C. | 4 | D. | 1 |
分析 先根据双曲线方程求得a和b,进而可得渐近线方程和定点坐标,根据定点到渐近线的距离等于$\frac{1}{5}$,进而求得m.
解答 解:根据双曲线方程可知a=$\frac{1}{3}$,b=$\sqrt{\frac{1}{m}}$,渐近线y=±$\frac{\sqrt{m}}{3}$x
取$\frac{\sqrt{m}}{3}$x-y=0,顶点(0,$\frac{1}{3}$),
∵双曲线9y2-mx2=1的一个顶点到它的一条渐近线的距离为$\frac{1}{5}$,
∴距离=$\frac{\frac{1}{3}}{\sqrt{\frac{m}{9}+1}}$=$\frac{1}{5}$
解得m=16
故选:B.
点评 本题主要考查了双曲线的简单性质.属基础题.

练习册系列答案
相关题目
6.若点(2a,a+1)在圆x2+(y-1)2=5的内部,则a的取值范围是( )
| A. | (-1,1) | B. | (0,1) | C. | (-1,$\frac{1}{5}$) | D. | (-$\frac{1}{5}$,1) |
4.幂函数y=xm(m∈Z)的图象如图所示,则m的值可以为( )


| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
11.底面为菱形的直棱柱ABCD-A1B1C1D1的两个对角面ACC1A1和BDD1B1的面积为6和8,则该棱柱的侧面积为( )
| A. | 18 | B. | 20 | C. | 36 | D. | 40 |
1.经过两圆x2+y2=9和(x+4)2+(y+3)2=8的交点的直线方程为( )
| A. | 8x+6y+13=0 | B. | 6x-8y+13=0 | C. | 4x+3y+13=0 | D. | 3x+4y+26=0 |
8.结论“对任意的x∈[1,2],x2-a≤0恒成立”成立的一个充分不必要条件是( )
| A. | a≥4 | B. | a≥5 | C. | a≤4 | D. | a≤5 |
5.已知一组数据为1、5、6、2、6,则这组数据的众数、中位数、平均数的大小关系为( )
| A. | 中位数>平均数>众数 | B. | 众数>中位数>平均数 | ||
| C. | 众数>平均数>中位数 | D. | 平均数>众数>中位数 |
6.不等式-25x2+10x-1≥0的解集为( )
| A. | ∅ | B. | $\left\{{x\left|{x=\frac{1}{5}}\right.}\right\}$ | C. | $\left\{{x\left|{x≠\frac{1}{5}}\right.}\right\}$ | D. | $\left\{{x\left|{x≤\frac{1}{5}}\right.}\right\}$ |
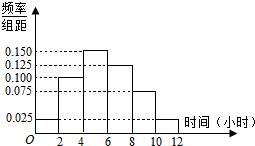 某校共有学生1600人,其中男生1000人,女生600人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集40位学生每周平均体育运动时间的样本数据(单位:小时).
某校共有学生1600人,其中男生1000人,女生600人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集40位学生每周平均体育运动时间的样本数据(单位:小时).