设θ为锐角.且$tanθ=\frac{{tan\frac{7π}{4}}}{{tan}}$.则θ的弧度数为$\frac{π}{6}$．题目和参考答案——青夏教育精英家教网—

题目内容

17．设θ为锐角，且$tanθ=\frac{{tan\frac{7π}{4}}}{{tan（-\frac{π}{3}）}}$，则θ的弧度数为$\frac{π}{6}$．

分析利用诱导公式与特殊角的三角函数值即可得出．

解答解：$tanθ=\frac{{tan\frac{7π}{4}}}{{tan（-\frac{π}{3}）}}$=$\frac{tan\frac{3π}{4}}{-tan\frac{π}{3}}$=$\frac{\sqrt{3}}{3}$，θ为锐角，
则θ=$\frac{π}{6}$．
故答案为：$\frac{π}{6}$．

点评本题考查了诱导公式与特殊角的三角函数值，考查了推理能力与计算能力，属于基础题．

练习册系列答案

相关题目

7．

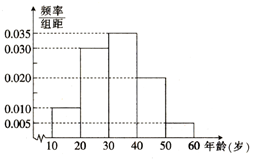随着医院对看病挂号的改革，网上预约成为了当前最热门的就诊方式，这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题；某医院研究人员对其所在地区年龄在10～60岁间的n位市民对网上预约挂号的了解情况作出调查，并将被调查的人员的年龄情况绘制成频率分布直方图，如右图所示．
（1）若被调查的人员年龄在20～30岁间的市民有300人，求被调查人员的年龄在40岁以上（含40岁）的市民人数；
（2）若按分层抽样的方法从年龄在[20，30）以内及[40，50）以内的市民中随机抽取10人，再从这10人中随机抽取3人进行调研，记随机抽的3人中，年龄在[40，50）以内的人数为X，求X的分布列以及数学期望．

8．命题“?x∈R，ax²-2ax+5＞0恒成立”是假命题，则实数a的取值范围是a＜0，或a≥5．

12．在函数$y=sin（x+\frac{π}{6}）$图象的对称轴中，与原点距离最小的一条的方程为x=$\frac{π}{3}$．

2．设函数$f（x）=\frac{1}{{\sqrt{a-x}}}$和g（x）=ln（-x²+4x-3）的定义域分别为集合A和B．
（1）当a=2，求函数y=f（x）+g（x）的定义域；
（2）若A∩（∁_RB）=A，求实数a的取值范围．

9．设定义域为R的偶函数f（x）满足：对任意的x₁，x₂∈（0，+∞），（x₁-x₂）[f（x₁）-f（x₂）]＞0，则f（-π）＞f（3.14）．（填“＞”、“＜”或“=”）

15．已知某几何体的三视图如图所示，则该几何体的体积为（　　）

16．已知函数f（x）是偶函数，当x＞0时，f（x）=-x²+x，那么当x＜0时，f（x）=（　　）

试题分类