题目内容
2．设函数$f（x）=\frac{1}{{\sqrt{a-x}}}$和g（x）=ln（-x2+4x-3）的定义域分别为集合A和B．（1）当a=2，求函数y=f（x）+g（x）的定义域；
（2）若A∩（∁RB）=A，求实数a的取值范围．
分析 （1）a=2时求出函数y=f（x）+g（x）的定义域即可；
（2）由集合A、B，根据补集与交集的定义，即可求出a的取值范围．
解答 解：（1）a=2时，函数$f（x）=\frac{1}{{\sqrt{a-x}}}$=$\frac{1}{\sqrt{2-x}}$，
g（x）=ln（-x2+4x-3），
∴函数y=f（x）+g（x）=$\frac{1}{\sqrt{2-x}}$+ln（-x2+4x-3），
应满足$\left\{\begin{array}{l}{2-x＞0}\\{{-x}^{2}+4x-3＞0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x＜2}\\{1＜x＜3}\end{array}\right.$，
即1＜x＜2，
∴函数y的定义域为（1，2）；
（2）∵A=（-∞，a），B=（1，3），
∴∁RB=（-∞，1]∪[3，+∞）；
若A∩（∁RB）=A，则a≤1，
∴实数a的取值范围是（-∞，1]．
点评 本题考查了求函数的定义域和集合的运算问题，是基础题目．
练习册系列答案
相关题目
13．已知△ABC，A，B，C所对的边分别为a，b，c，且acsinA＜$\overrightarrow{BA}•\overrightarrow{BC}$，则（ ）
| A． | △ABC是钝角三角形 | B． | △ABC是锐角三角形 | ||
| C． | △ABC是直角三角形 | D． | 无法判断 |
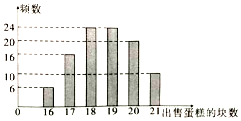某蛋糕店出售一种蛋糕，这种蛋糕的保质期很短，必须当天卖掉，否则容易变质，该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块，然后以每块26元的价格出售，如果当天卖不完，剩下的蛋糕只能以每块6元低价出售．蛋糕店记录了100天该种蛋糕的日需求量n（单位：块，n∈N*）整理得如图：