题目内容
9．设定义域为R的偶函数f（x）满足：对任意的x1，x2∈（0，+∞），（x1-x2）[f（x1）-f（x2）]＞0，则f（-π）＞f（3.14）．（填“＞”、“＜”或“=”）分析 根据已知分析出函数的单调性，结合函数f（x）是定义域为R的偶函数，可得答案．
解答 解：∵函数f（x）满足：对任意的x1，x2∈（0，+∞），（x1-x2）[f（x1）-f（x2）]＞0，
∴函数f（x）在（0，+∞）上为增函数，
又由函数f（x）是定义域为R的偶函数，
故f（-π）=f（π）＞f（3.14）．
故答案为：＞．
点评 本题考查的知识点是抽象函数及其应用，函数的单调性，函数的奇偶性，函数求值，难度中档
练习册系列答案
轻松暑假总复习系列答案
相关题目
19．
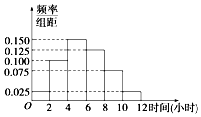某高校共有学生15000人，其中男生10500人，女生4500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）．
（1）应收集多少位女生的样本数据？
（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据的分组区间为：[0，2]，（2，4]，（4，6]，（6，8]，（8，10]，（10，12]
①估计该校学生每周平均体育运动时间超过4小时的概率P；
②假设该校每个学生每周平均体育运动时间超过4小时的概率都为P，试求从中任选三人至少有一人每周平均体育运动时间超过4小时的概率
（3）在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”．
附：K2=$\frac{n（ad-bc）2}{（a+b）（c+d）（a+c）（b+d）}$．
某高校共有学生15000人，其中男生10500人，女生4500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）．（1）应收集多少位女生的样本数据？
（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据的分组区间为：[0，2]，（2，4]，（4，6]，（6，8]，（8，10]，（10，12]
①估计该校学生每周平均体育运动时间超过4小时的概率P；
②假设该校每个学生每周平均体育运动时间超过4小时的概率都为P，试求从中任选三人至少有一人每周平均体育运动时间超过4小时的概率
（3）在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”．
| P（K2≥k0） | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| 男生 | 女生 | 总计 | |
| 每周平均体育运动时间不超过4小时 | 45 | 30 | 75 |
| 每周平均体育运动时间超过4小时 | 165 | 60 | 225 |
| 总计 | 210 | 90 | 300 |
10．设$f（x）=\left\{\begin{array}{l}{2^{x-2}}，x≤2\\{log_2}^{（x-1）}，x＞2\end{array}\right.$，则f[f（5）]=（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | 2 |
已知函数f（x）=2sin（2ωx+$\frac{π}{6}$）+1（其中0＜ω＜1），若点（-$\frac{π}{6}$，1）是函数f（x）图象的一个对称中心，
8．如图，给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2016}$的值的程序框图，其中判断框内可填入的是（ ）
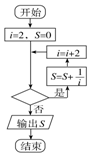
| A． | i≤2 021？ | B． | i≤2 019？ | C． | i≤2 017？ | D． | i≤2 015？ |