题目内容
在直角坐标系中,四边形OPQR的顶点按逆时针顺序依次为O(0,0)、P(1,t)、Q(1-2t,2+t)、R(-2t,2),其中t∈(0,+∞),试判断四边形OPQR的形状,并给出证明.
考点:直线的一般式方程与直线的垂直关系,直线的一般式方程与直线的平行关系
专题:直线与圆
分析:利用直线平行与垂直的条件及斜率公式可得kOP=kQR,kOR=kPQ,又kOP•kPQ=-1,即可得出结论.
解答:
解:∵O(0,0)、P(1,t)、Q(1-2t,2+t)、R(-2t,2),
∴由斜率公式得kOP=
=t,kQR=
=
=t,kOR=
=-
,kPQ=
=-
.
∴kOP=kQR,kOR=kPQ,从而OP∥QR,OR∥PQ.∴四边形OPQR为平行四边形.
又kOP•kPQ=-1,∴OP⊥PQ.
∴四边形OPQR为矩形.
∴由斜率公式得kOP=
| t-0 |
| 1-0 |
| 2-(2+t) |
| -2t-(1-2t) |
| -t |
| -1 |
| 2-0 |
| -2t-0 |
| 1 |
| t |
| 2+t-t |
| 1-2t-1 |
| 1 |
| t |
∴kOP=kQR,kOR=kPQ,从而OP∥QR,OR∥PQ.∴四边形OPQR为平行四边形.
又kOP•kPQ=-1,∴OP⊥PQ.
∴四边形OPQR为矩形.
点评:本题主要考查直线的斜率公式及直线平行垂直的判断方法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在平行四边形ABCD中,AB=4,AD=2,E,F分别是BC,CD的中点,且
•
=-15,则∠ABC=( )
| DE |
| BF |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知定义在[1-2a,2-a]上的偶函数f(x),当x≥0时,f(x)=x+ex,若f(t)<f(2t-1).则t的取值范围是( )
| A、[-1,1] | ||
| B、[0,1] | ||
C、[
| ||
D、[0,
|
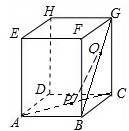 如图,正方体ABCD-EFGH的棱长为a,点P在AC上,点Q在BG上,AP=BQ=a,求证:PQ⊥AD.
如图,正方体ABCD-EFGH的棱长为a,点P在AC上,点Q在BG上,AP=BQ=a,求证:PQ⊥AD.