题目内容
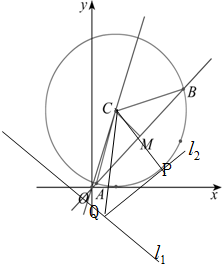
已知圆C与x轴相切,圆心C在射线3x-y=0(x>0)上,直线x-y=0被圆C截得的弦长为2
(1)求圆C标准方程;
(2)若点Q在直线l1:x+y+1=0上,经过点Q直线l2与圆C相切于p点,求|QP|的最小值.
| 7 |
(1)求圆C标准方程;
(2)若点Q在直线l1:x+y+1=0上,经过点Q直线l2与圆C相切于p点,求|QP|的最小值.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)设圆心坐标为 (a,3a),且a>0,求出圆心(a,3a)到直线x-y=0的距离,利用勾股定理,求出圆心与半径,即可求圆C标准方程;
(2)在Rt△QPC中,|QP|=
,所以,当|QC|最小时,|QP|有最小值.
(2)在Rt△QPC中,|QP|=
| (|QC|)2-9 |
解答:
 解:(1)因为圆心C在射线3x-y=0(x>0)上,
解:(1)因为圆心C在射线3x-y=0(x>0)上,
设圆心坐标为 (a,3a),且a>0,
圆心(a,3a)到直线x-y=0的距离为d=
=
a
又圆C与x轴相切,所以半径r=3a
设弦AB的中点为M,则|AM|=
在RtAMC中,得(
a)2+(
)2=(3a)2
解得a=1,r2=9
故所求的圆的方程是(x-1)2+(y-3)2=9 …(6分)
(2)如图,在Rt△QPC中,|QP|=
,
所以,当|QC|最小时,|QP|有最小值;
所以QC⊥l1于Q点时,|QC|min=
=
所以,|QP|min=
…..(12分)
 解:(1)因为圆心C在射线3x-y=0(x>0)上,
解:(1)因为圆心C在射线3x-y=0(x>0)上,设圆心坐标为 (a,3a),且a>0,
圆心(a,3a)到直线x-y=0的距离为d=
| |-2a| | ||
|
| 2 |
又圆C与x轴相切,所以半径r=3a
设弦AB的中点为M,则|AM|=
| 7 |
在RtAMC中,得(
| 2 |
| 7 |
解得a=1,r2=9
故所求的圆的方程是(x-1)2+(y-3)2=9 …(6分)
(2)如图,在Rt△QPC中,|QP|=
| (|QC|)2-9 |
所以,当|QC|最小时,|QP|有最小值;
所以QC⊥l1于Q点时,|QC|min=
| |1+3+1| | ||
|
5
| ||
| 2 |
所以,|QP|min=
| ||
| 2 |
点评:本题考查圆的方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
函数f(x)=
的定义域为( )
| 1 | ||
|
| A、(0,3) |
| B、(0,3] |
| C、(3,+∞) |
| D、[3,+∞) |
已知点A在球O的表面上,过点A的作平面α,使OA与平面α成30°角,若平面α截球所得的圆面积为3π,则球O的体积为( )
A、
| ||
| B、4π | ||
C、
| ||
| D、16π |
计算:(log213)3+(log217)3+3log213log217=( )
| A、0 | B、1 | C、-1 | D、2 |
某几何体的三视图如图所示,则该几何体的体积为( )
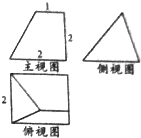

| A、2 | ||
B、
| ||
| C、3 | ||
D、
|