题目内容
 已知函数f(x)=|x+1|+|x-1|(x∈R).
已知函数f(x)=|x+1|+|x-1|(x∈R).(1)利用绝对值及分段函数知识,将函数解析式写成分段函数,然后在给定的坐标系中画出函数图象(不需列表);
(2)若函数f(x)在区间[a-1,2]上函数值随着自变量的增大而增大,试确定实数a的取值范围;
(3)若集合{x∈R|f(x)≥
| 1 |
| m |
考点:绝对值不等式的解法,带绝对值的函数
专题:函数的性质及应用
分析:(1)由绝对值的定义,在不同的范围内去绝对值,得当x<-1时,函数表达式为y=-2x;当-1≤x≤1时,函数表达式为y=2;当x>1时,函数表达式为y=2x.由此不难将函数化成分段函数的表示形式,并可作出它的图象.
(2)根据(1)的表达式,可得区间[a-1,2]是[1,+∞)的子集,由此建立不等式并解之,即可得到a的取值范围.
(2)根据(1)的表达式,可得区间[a-1,2]是[1,+∞)的子集,由此建立不等式并解之,即可得到a的取值范围.
解答:
解:(1)根据绝对值的定义,化简函数为
f(x)=|x+1|+|x-1|=
,
当x<-1时,函数图象是直线y=-2x的一部分;当-1≤x≤1时,函数图象是直线y=2的一部分;
当x>1时,函数图象是直线y=2x的一部分
由此可得函数的图象如下图
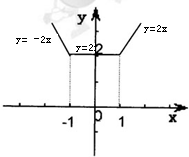
(2)由(1)得,函数的增区间为[1,+∞)
∵f(x)在区间[a-1,2]上单调递增,
∴1≤a-1<2,解之得2≤a<3
因此,实数a的取值范围为[2,3);
(3)由(1)图象得,要使集合{x∈R|f(x)≥
}=R,
只要
≤f(x)(min=2,解得m<0或者m≥
,
所以实数m的取值范围m<0或者m≥
.
f(x)=|x+1|+|x-1|=
|
当x<-1时,函数图象是直线y=-2x的一部分;当-1≤x≤1时,函数图象是直线y=2的一部分;
当x>1时,函数图象是直线y=2x的一部分
由此可得函数的图象如下图

(2)由(1)得,函数的增区间为[1,+∞)
∵f(x)在区间[a-1,2]上单调递增,
∴1≤a-1<2,解之得2≤a<3
因此,实数a的取值范围为[2,3);
(3)由(1)图象得,要使集合{x∈R|f(x)≥
| 1 |
| m |
只要
| 1 |
| m |
| 1 |
| 2 |
所以实数m的取值范围m<0或者m≥
| 1 |
| 2 |
点评:本题给出含有绝对值的函数,要求我们将其化成分段函数的表达式形式,并讨论它的单调区间,着重考查了绝对值的意义和函数的单调性以及函数图象的画法等知识,体现了数形结合的解题方法.

练习册系列答案
相关题目
函数f(x)=
的值域是( )
| 1 |
| 1+x2 |
| A、(0,1) |
| B、(0,1] |
| C、[0,1) |
| D、[0,1] |
已知f(x)=ax7+bx5-4,其中a,b味常数,若f(-3)=4,则f(3)的值等于( )
| A、-8 | B、-10 |
| C、-12 | D、-4 |
已知集合A={y|y=
,x>0},B={x|y=ln(2x-4)},若m∈A,m∉B,则实数m的取值范围是( )
| 1 |
| x |
| A、(-∞,0) |
| B、(2,+∞) |
| C、(0,2) |
| D、(0,2] |