题目内容
已知集合A={y|y=
，x＞0}，B={x|y=ln（2x-4）}，若m∈A，m∉B，则实数m的取值范围是（ ）
| 1 |
| x |
| A、（-∞，0） |
| B、（2，+∞） |
| C、（0，2） |
| D、（0，2] |
考点：元素与集合关系的判断
专题：集合
分析：先把集合A、B解出来，再由m∈A，m∉B，即求CAB．
解答：
解：A={y|y=
，x＞0}=（0，+∞），
B={x|y=ln（2x-4）}=（2，+∞），
由于m∈A，m∉B，
所以m∈CAB，
∴CAB=（0，2]，
故选D．
| 1 |
| x |
B={x|y=ln（2x-4）}=（2，+∞），
由于m∈A，m∉B，
所以m∈CAB，
∴CAB=（0，2]，
故选D．
点评：本题主要考查元素与集合的关系，属于基础题．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
已知函数f（x）=|x+1|+|x-1|（x∈R）．若f（x）=2x，g（x）=log2x，则如上图所示的程序框图中，输入x=4，输出h（x）=（ ）
| A、16 | ||
B、
| ||
| C、2 | ||
D、
|
设复数z满足z•i=2015-i，i为虚数单位，则在复平面内，复数z对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设集合A={-1，0，1}，B={x∈R|x＞0}，则A∩B=（ ）
| A、{-1，0} | B、{-1} |
| C、{0，1} | D、{1} |
某几何体的三视图如图所示，则它的体积为（ ）
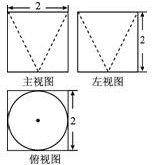
A、8-
| ||
B、8-
| ||
| C、8-2π | ||
D、
|