题目内容
 椭圆C:
椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆C的方程;
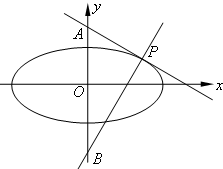
(2)点P是椭圆C上除长轴、短轴端点外的任一点,过点P作直线l,使得l与椭圆C有且只有一个公共点,设l与y轴的交点为A,过点P作与l垂直的直线m,设m与y轴的交点为B,求证:△PAB的外接圆经过定点.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)将x=-c代入椭圆方程
+
=1,得y=±
.由题意知2
=1,e=
=
,由此能求出椭圆C的方程.
(2)设P(x0,y0)(y0≠0),直线l的方程为y-y0=k(x-x0).联立
,得(1+4k2)x2+8(ky0-k2x0)x+4(y02-2kx0y0+k2x02-1)=0,由此能证明△PAB的外接圆经过定点.
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
| b2 |
| a |
| c |
| a |
| ||
| 2 |
(2)设P(x0,y0)(y0≠0),直线l的方程为y-y0=k(x-x0).联立
|
解答:
(1)解:由于c2=a2-b2,
将x=-c代入椭圆方程
+
=1,得y=±
.
由题意知2
=1,即a=2b2,
又e=
=
,∴a=2,b=1.
∴椭圆C的方程为
+y2=1.
(2)证明:设P(x0,y0)(y0≠0),
则直线l的方程为y-y0=k(x-x0).
联立
,
整理得(1+4k2)x2+8(ky0-k2x0)x+4(y02-2kx0y0+k2x02-1)=0.
由题意△=0,即(4-x02)k2+2x0y0k+1-y02=0.
又
+
=1,∴16y02k2+8x0y0k+x02=0,∴k=-
.
所以直线l方程为
+y0y=1,令x=0,解得点A(0,
),
又直线m方程为y=
x-3y0,令x=0,解得点B(0,-3y0),
△PAB的外接圆方程为以AB为直径的圆方程,即x2+(y-
)(y+3y0)=0.
整理得:x2+y2-3+y(3y0-
)=0,分别令
,
解得圆过定点(±
,0).
∴△PAB的外接圆经过定点(±
,0).
将x=-c代入椭圆方程
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
由题意知2
| b2 |
| a |
又e=
| c |
| a |
| ||
| 2 |
∴椭圆C的方程为
| x2 |
| 4 |
(2)证明:设P(x0,y0)(y0≠0),
则直线l的方程为y-y0=k(x-x0).
联立
|
整理得(1+4k2)x2+8(ky0-k2x0)x+4(y02-2kx0y0+k2x02-1)=0.
由题意△=0,即(4-x02)k2+2x0y0k+1-y02=0.
又
| ||
| 4 |
| y | 2 0 |
| x0 |
| 4y0 |
所以直线l方程为
| x0x |
| 4 |
| 1 |
| y0 |
又直线m方程为y=
| 4y0 |
| x0 |
△PAB的外接圆方程为以AB为直径的圆方程,即x2+(y-
| 1 |
| y0 |
整理得:x2+y2-3+y(3y0-
| 1 |
| y0 |
|
解得圆过定点(±
| 3 |
∴△PAB的外接圆经过定点(±
| 3 |
点评:本题考查椭圆方程的求法,考查三角形的外接圆过定点的证明,解题时要认真审题,注意直线与椭圆的位置关系的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=3-2sin22x的最小正周期为( )
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
 若椭圆E1:
若椭圆E1: 如图,在四棱锥S-ABCD中,地面ABCD为矩形,侧面SAD为边长2的正三角形,且面SAD⊥面ABCD.AB=
如图,在四棱锥S-ABCD中,地面ABCD为矩形,侧面SAD为边长2的正三角形,且面SAD⊥面ABCD.AB=