题目内容
已知圆C的圆心C(-1,2),且圆C经过原点.
(1)求圆C的方程;
(2)过原点作圆C的切线m,求切线m的方程;
(3)过点A(-2,0)的直线n被圆C截得的弦长为2,求直线n的方程.
(1)求圆C的方程;
(2)过原点作圆C的切线m,求切线m的方程;
(3)过点A(-2,0)的直线n被圆C截得的弦长为2,求直线n的方程.
考点:圆的切线方程,直线与圆的位置关系
专题:直线与圆
分析:(1)由条件求得圆的半径,可得要求的圆的方程.
(2)设圆的切线方程为y=kx,由圆心到切线的距离等于半径求得k的值,可得圆切线方程.
(3)用点斜式设出直线n的方程,由弦长为2,半径为
,可得弦心距为2,即圆心(-1,2)到直线n的距离为2,由此利用点到直线的距离公式求得k的值,可得直线n的方程.
(2)设圆的切线方程为y=kx,由圆心到切线的距离等于半径求得k的值,可得圆切线方程.
(3)用点斜式设出直线n的方程,由弦长为2,半径为
| 5 |
解答:
解:(1)圆的半径为
=
,故要求的圆的方程为(x+1)2+(y-2)2=5.
(2)设圆的切线方程为y=kx,由圆心到切线的距离等于半径可得
=
,
求得k=
,故圆切线方程为y=
x.
(3)设直线n的方程为 y-0=k(x+2),即kx-y+2k=0,由弦长为2,半径为
,可得弦心距为2,
即圆心(-1,2)到直线n的距离为2,即
=2,求得k=0,或k=-
.
直线n的方程为y=0或 4x+3y+8=0.
| 1+4 |
| 5 |
(2)设圆的切线方程为y=kx,由圆心到切线的距离等于半径可得
| |-k-2| | ||
|
| 5 |
求得k=
| 1 |
| 2 |
| 1 |
| 2 |
(3)设直线n的方程为 y-0=k(x+2),即kx-y+2k=0,由弦长为2,半径为
| 5 |
即圆心(-1,2)到直线n的距离为2,即
| |-k-2+2k| | ||
|
| 4 |
| 3 |
直线n的方程为y=0或 4x+3y+8=0.
点评:本题主要考查求圆的标准方程,直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
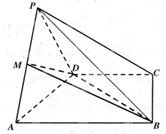 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.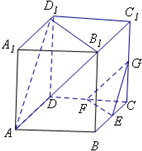 如图,在正方体ABCD=A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
如图,在正方体ABCD=A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.