题目内容
已知二次函数f(x)的最小值为-4且关于x的不等式f(x)<0的解集为{x|-1≤x≤3,x∈R},
(1)求函数f(x)的解析式;
(2)求函数g(x)=
-lnx的零点个数.
(1)求函数f(x)的解析式;
(2)求函数g(x)=
| f(x) |
| x |
考点:根的存在性及根的个数判断,函数解析式的求解及常用方法,利用导数研究函数的极值
专题:函数的性质及应用,不等式的解法及应用
分析:(1)根据二次函数的大小,方程,与函数的解析式的关系,求解系数.
(2)g′(x)=1+
-
=
.根据导数判断单调性即可求解.
(2)g′(x)=1+
| 3 |
| x2 |
| 4 |
| x |
| (x-1)(x-3) |
| x2 |
解答:
解:(1)f(x)是二次函数,且关于x的不等式f(x)的解集为
{x|-1≤x≤3,x∈R},∴f(x)=a(x+1)(x-3)=ax2-2ax-3a,且a>0.
a>0,f(x)=a[(x-1)2-4]≥-4且f(1)=-4a,∴f(x)min=-4a=-4,a=-1,
故函数f(x)的解析式为f(x)=x2-2x-3
(2)g(x)=
-4lnx=x-
-4lnx-2,(x>0),∴g′(x)=1+
-
=
.
x,g′(x),g(x)的取值变化情况如下:
当0<x≤3时,g(x)≤g(1)=-4<0;又g(e5)=e5-
-20-2>25-1-22=9.
故函数g(x)只有1个零点,且零点x0∈(3,e5).
{x|-1≤x≤3,x∈R},∴f(x)=a(x+1)(x-3)=ax2-2ax-3a,且a>0.
a>0,f(x)=a[(x-1)2-4]≥-4且f(1)=-4a,∴f(x)min=-4a=-4,a=-1,
故函数f(x)的解析式为f(x)=x2-2x-3
(2)g(x)=
| x2-2x-3 |
| x |
| 3 |
| x |
| 3 |
| x2 |
| 4 |
| x |
| (x-1)(x-3) |
| x2 |
x,g′(x),g(x)的取值变化情况如下:
| x | (0,1) | 1 | (1,3) | 3 | (3,+∞ |
| g′(x) | + | 0 | - | 0 | + |
| g(x) | 单调增加 | 极大值 | 单调减少 | 极小值 | 单调增加 |
| 3 |
| e5 |
故函数g(x)只有1个零点,且零点x0∈(3,e5).
点评:本题考查了函数解析式的求解,导数的运用,属于综合题,难度较大

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=sin(-2x)的一个单调增区间是( )
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
若α∈(
,π),且cos2α=sin(
-α),则sin2α的值为( )
| π |
| 2 |
| π |
| 4 |
A、-
| ||
B、
| ||
| C、1 | ||
| D、-1 |
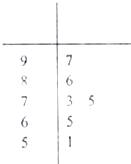 某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.
某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.