题目内容

已知向量
a
=（
3
，1），且单位向量
b
与
a
的夹角为60°，则
b
的坐标为
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：设
b
的坐标为（x，y），根据向量的数量积
a
•
b
=|
a
|•|
b
|cos＜
a
，
b
＞，和向量的模，构造方程组，解得即可．
解答： 解：向量
b
单位向量，则|
b
|=1，设
b
的坐标为（x，y），
∴x2+y2=1，①
∵
a
=（
3
，1），
∴|
a
|=2，
∴
a
•
b
=|
a
|•|
b
|cos＜
a
，
b
＞=2×1×cos60°=1，
∴
a
•
b
=（
3
，1）（x，y）=
3
x+y=1，②
由①②构成方程组，
解得，
x=0
y=1
或
x=
3
2
y=
1
2

故答案为：（0，1），（
3
2
，
1
2
）
点评：本题考查向量的数量积公式，以及利用数量积求两个向量的夹角问题，根据题意求出
a
•
b
是解题的关键，属基础题
练习册系列答案
相关题目
已知函数f（x）=ax2+bx+c（a≠0）的图象关于直线x=-
b
2a
对称，则方程m[f（x）]2+nf（x）+p的根是否关于x=-
b
2a
对称（a，b，c，m，n，p为任意非零实数）？
若向量
a
=（x+1，2）和向量
b
=（1，-1）平行，则|
a
+
b
|=
 
．
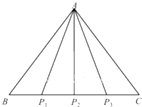如图所示，△ABC是边长为1的正三角形，且点P在边BC上运动．当
PA
•
PC
取得最小值时，则cos∠PAB的值为
 
．
把直线λx-y+2=0按向量
a
=（2，0）平移后恰与x2+y2-4y+2x-2=0相切，则实数λ的值为
 
．
若数列{an}满足
an+2
an+1
+
an+1
an
=k（k为常数），则称数列{an}为等比和数列，k称为公比和，已知数列{an}是以3为公比和的等比和数列，其中a1=1，a2=2，则a2013=
 
．
在△ABC中，若sinA：sinB：sinC=1：2：
6
，则最大角的余弦值为
 
．
若f（x）=ax3+x恰有三个单调区间，则a的取值范围为
 
．
已知x、y满足约束条件
2x-y+1≥0
2x+y≥0
x≤1
，则z=x+3y的最小值为（　　）
A、7
B、
5
3
C、-5
D、5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网