题目内容

用1，2，3，4，5，6，7七个数字排列组成七位数，使其中偶位数上必定是偶数，那么可得七位数的个数是（　　）
A、A44
B、A44A33
C、6A33
D、C152C403A55
考点：计数原理的应用
专题：排列组合
分析：分两步完成，先排偶数位有A33种种方法，再排奇数位有A44种方法，根据分步计数原理得到
解答： 解：1，2，3，4，5，6，7七个数字排列组成七位数，使其中偶位数上必定是偶数，分两步完成：
第一步先排偶数位，有2，4，6，三个数可选，有A33种方法，
第二步排计数位，有1，3，5，7，四个数在可选，有A44种方法．
根据分步计数原理，所求可得七位数的个数A44A33．
故选B．
点评：本题主要考查分步计数原理的应用，属于基础题
练习册系列答案
相关题目
如图，?ABCD中，点M是AB的中点，CM与BD相交于点N，若
BN
=λ
BD
，求实数λ的值．
四棱柱ABCD-A1B1C1D1的三视图和直观图如下：

（1）求出该四棱柱的表面积；
（2）设E是DC上一点，试确定E的位置，使D1E∥平面A1BD，并说明理由．
某校数学课外小组在坐标纸上，为学校的一块空地设计植树方案如下：第k棵树种植在点Pk（xk，yk）处，其中x1=1，y1=1，当k≥2时，
xk=xk-1+1-5[T(
k-1
5
)-T(
k-2
5
)]
yk=yk-1+T(
k-1
5
)-T(
k-2
5
)
，T（a）表示非负实数a的整数部分，例如T（2.6）=2，T（0.2）=0．按此方案，第6棵树种植点的坐标应为
 
；第2013棵树种植点的坐标应为
 
．
已知数列{an}：a1，a2，a3，…，an，如果数列{bn}：b1，b2，b3，…，bn满足b1=an，bk=ak-1+ak-bk-1，其中k=2，3，…n，则称{bn}为{an}的“衍生数列”．若数列{an}：a1，a2，a3，a4，的“衍生数列”是5，-2，7，2，则{an}为
 
；若n为偶数，且{an}的“衍生数列”是{bn}，则{bn}的“衍生数列”是
 
．
从10名女学生中选2名，40名男生中选3名，担任五种不同的职务，规定女生不担任其中某种职务，不同的分配方案有（　　）
A、A102A403
B、C102A31A44C403
C、C152C403A55
D、C102C403
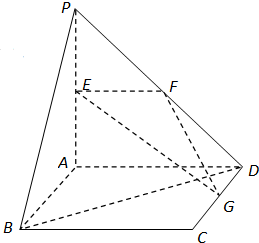如图，直线PA⊥平面ABCD，四边形ABCD是正方形，且PA=AD=2，点E、F、G分别是线段PA、PD、CD的中点．
（1）求异面直线EG与BD所成角的大小（结果用反三角表示）；
（2）在线段CD上是否存在一点Q，使BF⊥EQ，若存在，求出DQ的长，若不存在，请说明理由．
如图，正方体ABCD-A1B1C1D中，异面直线AD1与A1B所成的角的大小是
 
．
在△ABC中，角A、B、C所对的边分别为a，b，c．设向量
m
=(a，cosB)，
n
=(b，cosA)，且
m
∥
n
，
m
≠
n
．求sinA+sinB的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网