题目内容
已知数列{an}中,a1=1,an+1=(1+
)an+
,n∈N*.
(1)求证:当n≥2且n∈N*时,an≥3;
(2)求证:an<e3,n∈N*(e为自然对数的底数,参考数据ln3<1.1,ln4<1.4).
| 1 |
| n2 |
| 1 |
| 3n-1 |
(1)求证:当n≥2且n∈N*时,an≥3;
(2)求证:an<e3,n∈N*(e为自然对数的底数,参考数据ln3<1.1,ln4<1.4).
考点:数列与不等式的综合,数列递推式,数列与函数的综合,数学归纳法
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:( I)证明:方法一:通过已知条件以及an+1=(1+
)an+
,推出an>0,化简an+1-an得到an+1>an(n∈N*),然后证明an≥3(n≥2).
方法二:利用数学归纳法的步骤直接证明即可.
( II)证明:由( I)推出an+1≤(1+
+
)an,两边取自然对数得lnan+1≤lnan+ln(1+
+
),构造f(x)=ln(1+x)-x(x≥0),求解导数f′(x)=
-1=
<0恒成立,转化为f(x)为[0,+∞)上的减函数,通过放缩法得到lnan+1-lnan<
-
+
(n≥2),通过求和与放缩推出lnan-lna2<
(n≥3),然后证明an<e3(n∈N*).
| 1 |
| n2 |
| 1 |
| 3n-1 |
方法二:利用数学归纳法的步骤直接证明即可.
( II)证明:由( I)推出an+1≤(1+
| 1 |
| n2 |
| 1 |
| 3n-1 |
| 1 |
| n2 |
| 1 |
| 3n-1 |
| 1 |
| 1+x |
| -x |
| 1+x |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| 3n-1 |
| 3 |
| 2 |
解答:
(本小题满分12分)
( I)证明:方法一:
∵a1=1>0,由an+1=(1+
)an+
得a2>0,
于是易得an>0.…(2分)
又an+1-an=
+
>0(n∈N*),即an+1>an(n∈N*)又∵a2=3,∴an≥a2=3(n≥2).…(4分)
方法二:数学归纳法
(1)当n=2时,an=a2=3≥3,命题成立.…(1分)
(2)假设当n=k(n≥2)时命题成立,即ak≥3,
当n=k+1时,ak+1=(1+
)ak+
=ak+
+
>ak≥3∴n=k+1时命题成立.…(3分)
由(1)(2)可知,当n≥2时,an≥3.…(4分)
( II)证明:由( I)知an+1=(1+
)an+
≤(1+
)an+
=(1+
+
)an,…(5分)
两边取自然对数得:lnan+1≤lnan+ln(1+
+
).…(6分)
令f(x)=ln(1+x)-x(x≥0),
则当x>0时,f′(x)=
-1=
<0恒成立,
∴f(x)为[0.+∞)上的减函数,∴f(x)≤f(0)=0∴ln(1+x)<x在x>0时恒成立,…(7分)lnan+1<lnan+
+
<lnan+
+
=lnan+
-
+
即lnan+1-lnan<
-
+
(n≥2),…(9分)
故,lnan-lnan-1<
-
+
,lnan-1-lnan-2<
-
+
…lna3-lna2<1-
+
,以上各式相加得:lnan-lna2<1-
+
<1+
=
,(n≥3)…(10分)
又∵a2=3,∴lnan<
+ln3<3,∴an<e3(n≥3),…(11分)
又∵a1=1<e3,a2=3<e3,
∴an<e3(n∈N*).…(12分)
( I)证明:方法一:
∵a1=1>0,由an+1=(1+
| 1 |
| n2 |
| 1 |
| 3n-1 |
于是易得an>0.…(2分)
又an+1-an=
| an |
| n2 |
| 1 |
| 3n-1 |
方法二:数学归纳法
(1)当n=2时,an=a2=3≥3,命题成立.…(1分)
(2)假设当n=k(n≥2)时命题成立,即ak≥3,
当n=k+1时,ak+1=(1+
| 1 |
| k2 |
| 1 |
| 3k-1 |
| ak |
| k2 |
| 1 |
| 3k-1 |
由(1)(2)可知,当n≥2时,an≥3.…(4分)
( II)证明:由( I)知an+1=(1+
| 1 |
| n2 |
| 1 |
| 3n-1 |
| 1 |
| n2 |
| an |
| 3n-1 |
| 1 |
| n2 |
| 1 |
| 3n-1 |
两边取自然对数得:lnan+1≤lnan+ln(1+
| 1 |
| n2 |
| 1 |
| 3n-1 |
令f(x)=ln(1+x)-x(x≥0),
则当x>0时,f′(x)=
| 1 |
| 1+x |
| -x |
| 1+x |
∴f(x)为[0.+∞)上的减函数,∴f(x)≤f(0)=0∴ln(1+x)<x在x>0时恒成立,…(7分)lnan+1<lnan+
| 1 |
| n2 |
| 1 |
| 3n-1 |
| 1 |
| n(n-1) |
| 1 |
| 3n-1 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| 3n-1 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| 3n-1 |
故,lnan-lnan-1<
| 1 |
| n-2 |
| 1 |
| n-1 |
| 1 |
| 3n-2 |
| 1 |
| n-3 |
| 1 |
| n-2 |
| 1 |
| 3n-3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| ||||
1-
|
| 1 |
| 2 |
| 3 |
| 2 |
又∵a2=3,∴lnan<
| 3 |
| 2 |
又∵a1=1<e3,a2=3<e3,
∴an<e3(n∈N*).…(12分)
点评:本题考查数列与不等式的综合应用,数列与函数的综合应用,数学归纳法的证明方法,放缩法的证明方法,数列的求和,考查分析问题解决问题的能力,转化思想的应用,是难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知数列{an}的通项公式为an=2n(n∈N*),现将该数列{an}的各项排列成如图的三角数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )
已知数列{an}的通项公式为an=2n(n∈N*),现将该数列{an}的各项排列成如图的三角数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )| A、M(46,16) |
| B、M(46,25) |
| C、M(45,15) |
| D、M(45,25) |
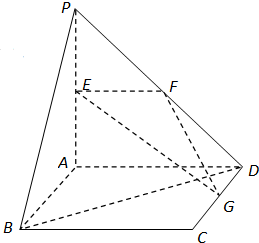 如图,直线PA⊥平面ABCD,四边形ABCD是正方形,且PA=AD=2,点E、F、G分别是线段PA、PD、CD的中点.
如图,直线PA⊥平面ABCD,四边形ABCD是正方形,且PA=AD=2,点E、F、G分别是线段PA、PD、CD的中点.