题目内容
已知椭圆C的中心在坐标原点，一个焦点为F（0，-2
），对应的准线方程为y=-
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在直线l，使l与椭圆C交于不同的两点M，N，且使线段MN恰好被直线x=-
平分？若存在，求l的倾斜角θ的取值范围，若不存在，说明理由．
| 2 |
9
| ||
| 4 |
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在直线l，使l与椭圆C交于不同的两点M，N，且使线段MN恰好被直线x=-
| 1 |
| 2 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：（Ⅰ）设椭圆方程为
+
=1，从而求出a，b，c，从而求椭圆的方程；
（Ⅱ）设存在直线l：y=kx+b．故椭圆交于M，N，线段MN中点为P（x0，y0）；从而求l的倾斜角θ的取值范围．
| y2 |
| a2 |
| x2 |
| b2 |
（Ⅱ）设存在直线l：y=kx+b．故椭圆交于M，N，线段MN中点为P（x0，y0）；从而求l的倾斜角θ的取值范围．
解答：
解：（Ⅰ）设椭圆方程为
+
=1；
由题意c=2
，
=
⇒a2=9，b2=1．
∴椭圆方程为x2+
=1
（Ⅱ）设存在直线l：y=kx+b．故椭圆交于M，N，线段MN中点为P（x0，y0）．
由
⇒(9+k2)x2+2kbx+b2-9=0
则判别式△=4k2b2-4（9+k2）（b2-9）=-36（b2-k2-9）＞0
得 b2-k2-9＜0①
又
=-
=-
⇒b=
．代入①
解得 k＞
或k＜-
，
∴θ∈(
，
)∪(
，
)．
| y2 |
| a2 |
| x2 |
| b2 |
由题意c=2
| 2 |
| a2 | ||
2
|
9
| ||
| 4 |
∴椭圆方程为x2+
| y2 |
| 9 |
（Ⅱ）设存在直线l：y=kx+b．故椭圆交于M，N，线段MN中点为P（x0，y0）．
由
|
则判别式△=4k2b2-4（9+k2）（b2-9）=-36（b2-k2-9）＞0
得 b2-k2-9＜0①
又
| x1+x2 |
| 2 |
| kb |
| 9+k2 |
| 1 |
| 2 |
| 9+k2 |
| 2k |
解得 k＞
| 3 |
| 3 |
∴θ∈(
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
点评：本题考查了圆锥曲线与直线的关系应用，属于基础题．
练习册系列答案
黄冈创优卷系列答案
相关题目
已知f（x）是定义在[a，b]上的函数，其图象是一条连续的曲线，且满足下列条件：
①f（x）的值域为M，且M⊆[a，b]；
②对任意不相等的x，y∈[a，b]，都有|f（x）-f（y）|＜|x-y|．
那么，关于x的方程f（x）=x在区间[a，b]上根的情况是（ ）
①f（x）的值域为M，且M⊆[a，b]；
②对任意不相等的x，y∈[a，b]，都有|f（x）-f（y）|＜|x-y|．
那么，关于x的方程f（x）=x在区间[a，b]上根的情况是（ ）
| A、没有实数根 |
| B、有且仅有一个实数根 |
| C、恰有两个不等的实数根 |
| D、实数根的个数无法确定 |
下列命题错误的是（ ）
| A、命题“若x2+y2≠0，则x=y=0”的逆否命题为“若x，y中至少有一个不为0，则x2+y2≠0” |
| B、若命题p：?x0∈R，使得x02-x0+1≤0；则￢p：?x∈R，均有x2-x+1＞0 |
| C、若p∧q为假命题，则p∨￢q为真命题 |
| D、“x＞|y|”是“x2＞y2”的充分不必要条件 |
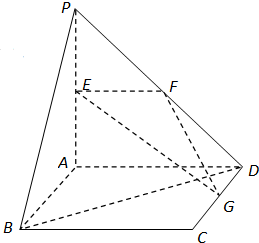如图，直线PA⊥平面ABCD，四边形ABCD是正方形，且PA=AD=2，点E、F、G分别是线段PA、PD、CD的中点．