题目内容
5.已知t>0,关于x的方程$\sqrt{2}-|x|=\sqrt{t-{x^2}}$,则这个方程的实数的个数是( )| A. | 0或2 | B. | 0或2或3或4 | C. | 0或2或4 | D. | 0或1或2或3或4 |
分析 因为关于x的方程$\sqrt{2}-|x|=\sqrt{t-{x^2}}$等号两边均为正数,转化为C1:y=|x|-$\sqrt{2}$,C2:y=-$\sqrt{t-{x}^{2}}$的图象的交点问题,可通过在同一坐标系中做出函数C1:y=|x|-$\sqrt{2}$,C2:y=-$\sqrt{t-{x}^{2}}$,的图象,通过判断图象交点个数来判断方程的相异实根根数.
解答  解:令C1:y=|x|-$\sqrt{2}$,C2:y=-$\sqrt{t-{x}^{2}}$,
解:令C1:y=|x|-$\sqrt{2}$,C2:y=-$\sqrt{t-{x}^{2}}$,
由于y=|x|-$\sqrt{2}$=$\left\{\begin{array}{l}{x-\sqrt{2},x≥0}\\{-x-\sqrt{2},x<0}\end{array}\right.$,
方程y=-$\sqrt{t-{x}^{2}}$平方得:x2+y2=t,(y≤0),
画出它们的图象,如图所示,一个是折线,一个是半个圆.
当圆心(0,0)到直线y=x-$\sqrt{2}$的距离等于半径时,
即$\frac{|-\sqrt{2}|}{\sqrt{2}}$=1=$\sqrt{t}$时,t=1;
当圆经过点(0,-$\sqrt{2}$)时,02+(-$\sqrt{2}$)2=t,⇒t=2.
利用数形结合知:当0<t<1或t>2时,方程无实数根;
当t=1时,方程有2个实数根;
当t=2时,方程有3个实数根;
当1<t<2时,方程有4个实数根.
综合,则这个方程实根的个数情况是 0或2或3或4.
故选:B.
点评 本题主要考查图象法判断方程的实根个数,关键是画出两个函数的图象.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
15.命题“若x=3,则x2-9x+18=0”的逆命题、否命题和逆否命题中,假命题的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
10.已知xy>0,则$\frac{y}{x+y}+\frac{2x}{2x+y}$的最小值为( )
| A. | $4+2\sqrt{2}$ | B. | $4-2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | 1 |
17.已知z∈C,“$z+\overline z=0$”是“z为纯虚数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.函数f(x)=ln|1-x|的图象大致形状是( )
| A. |  | B. |  | C. |  | D. |  |
15.已知集合$M=\left\{{x\left|{\frac{x-5}{x+1}≤0}\right.}\right\}$,N={-3,-1,1,3,5},则M∩N=( )
| A. | {-3,-1,1,3,5} | B. | {-1,1,3,5} | C. | {1,3,5} | D. | {-3,-1,1,3,} |
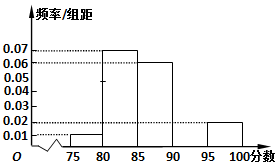 某高校在2016年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2016年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.