题目内容
16.已知数列{an}前n项和为Sn,满足${S_n}=2{a_n}-2n(n∈{N^*})$(1)证明:{an+2}是等比数列,并求{an}的通项公式;
(2)数列{bn}满足${b_n}=log_2^{{a_n}+2}$,Tn为数列$\left\{{\frac{1}{{{b_n}{b_{n+1}}}}}\right\}$的前n项和,若Tn<a对正实数a都成立,求a的取值范围.
分析 (1)利用数列递推关系、等比数列的通项公式即可得出.
(2)利用“裂项求和”方法即可得出.
解答 解:(1)证明:由题设${S_n}=2{a_n}-2n(n∈{N^*}),{S_{n+1}}=2{a_{n-1}}-2(n-1)(n≥2)$,
两式相减得an=2an-1+2…(2分)
即an+2=2(an-1+2)又a1+2=4,所以{an+2}是以4为首项,2为公比的等比数列…(4分)${a_n}+2=4×{2^{n-1}},{a_n}=4×{2^{n-1}}-2={2^{n+1}}-2(n≥2)$
又a1=2,所以${a_n}={2^{n+1}}-2(n∈{N^*})$…(6分)
(2)∵${b_n}=log_2^{{a_n}+2}$=$lo{g}_{2}{2}^{n+1}$=n+1.
∴$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{(n+1)(n+2)}$=$\frac{1}{n+1}$-$\frac{1}{n+2}$.…(8分)
所以${T_n}=(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+…+(\frac{1}{n+1}-\frac{1}{n+2})=\frac{1}{2}-\frac{1}{n+2}<\frac{1}{2}$…(10分)
依题意得:$a≥\frac{1}{2}$…(12分)
点评 本题考查了数列递推关系、等比数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.将4个不同的小球装入4个不同的盒子,则在至少一个盒子为空的条件下,恰好有两个盒子为空的概率是( )
| A. | $\frac{21}{58}$ | B. | $\frac{12}{29}$ | C. | $\frac{21}{64}$ | D. | $\frac{7}{27}$ |
5.已知t>0,关于x的方程$\sqrt{2}-|x|=\sqrt{t-{x^2}}$,则这个方程的实数的个数是( )
| A. | 0或2 | B. | 0或2或3或4 | C. | 0或2或4 | D. | 0或1或2或3或4 |
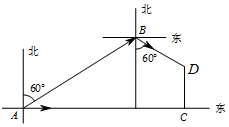 如图,船甲以每小时30公里的速度向正东航行,船甲在A处看到另一船乙在北偏东60°的方向上的B处,且$AB=30\sqrt{3}$公里,正以每小时$5\sqrt{3}$公里的速度向南偏东60°的方向航行,行驶2小时后,甲、乙两船分别到达C、D处,则CD等于$10\sqrt{3}$公里.
如图,船甲以每小时30公里的速度向正东航行,船甲在A处看到另一船乙在北偏东60°的方向上的B处,且$AB=30\sqrt{3}$公里,正以每小时$5\sqrt{3}$公里的速度向南偏东60°的方向航行,行驶2小时后,甲、乙两船分别到达C、D处,则CD等于$10\sqrt{3}$公里.