题目内容
13.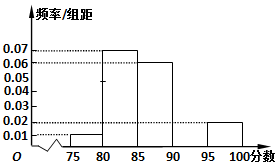 某高校在2016年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2016年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.(1)求出第4组的频率;
(2)根据样本频率分布直方图估计样本的中位数;
(3)如果从“优秀”和“良好”的学生中分别选出3人与2人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
分析 (1)由频率分布直方图能求出第4组的频率.
(2)由频率分布直方图能估计样本的中位数.
(3)从“优秀”和“良好”的学生中分别选出3人与2人,再从这5人中选2人,基本事件总数n=${C}_{5}^{2}$=10,至少有一人是“优秀”的对立事件是两人都是良好,由此能求出至少有一人是“优秀”的概率.
解答 解:(1)由频率分布直方图得:
第4组的频率为:p=1-(0.01+0.07+0.06+0.02)×5=0.2.
(2)由频率分布直方图得:
[75,85)的频率为(0.01+0.07)×5=0.4,
[85,90)的频率为:0.06×5=0.3,
∴根据样本频率分布直方图估计样本的中位数为:
85+$\frac{0.5-0.4}{0.3}×5$=$\frac{250}{3}$.
(3)从“优秀”和“良好”的学生中分别选出3人与2人,
再从这5人中选2人,
基本事件总数n=${C}_{5}^{2}$=10,
至少有一人是“优秀”的对立事件是两人都是良好,
∴至少有一人是“优秀”的概率p=1-$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{9}{10}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,考查古典概型的概率计算,属于基础题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
18.设$a={log_{\frac{1}{3}}}\frac{1}{2},b={log_{\frac{1}{2}}}\frac{1}{3},c={log_3}\frac{4}{3}$,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | b<c<a |
5.已知t>0,关于x的方程$\sqrt{2}-|x|=\sqrt{t-{x^2}}$,则这个方程的实数的个数是( )
| A. | 0或2 | B. | 0或2或3或4 | C. | 0或2或4 | D. | 0或1或2或3或4 |
2.函数$f(x)=ax-\frac{1}{2}{x^2}-4lnx$在区间[1,+∞)上为减函数,则实数a的取值范围是( )
| A. | (-∞,4) | B. | (-∞,4] | C. | (-∞,5) | D. | (-∞,5] |
3.某几何体的三视图如图所示,则其体积为( )
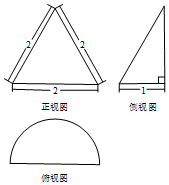

| A. | $\frac{{\sqrt{3}π}}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{{\sqrt{3}π}}{6}$ | D. | $\frac{{\sqrt{3}π}}{3}$ |