题目内容
函数y=2x-3+
的值域为 .
| 4x-13 |
考点:函数的值域
专题:计算题
分析:先进行换元,令t=
,把已知函数可转化为关于t的二次函数,结合t的范围及二次函数的性质可求解
| 4x-13 |
解答:
解:令t=
,则t≥0且x=
∴y=
-3+t=
t2+t+
=
(t+1)2+3
根据二次函数的性质可知,函数在[0,+∞)上单调递增
故当t=0即x=
时函数有最小值
,函数没有最大值
故函数的值域为[
,+∞)
故答案为:[
,+∞)
| 4x-13 |
| 13+t2 |
| 4 |
∴y=
| 13+t2 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
根据二次函数的性质可知,函数在[0,+∞)上单调递增
故当t=0即x=
| 13 |
| 4 |
| 7 |
| 2 |
故函数的值域为[
| 7 |
| 2 |
故答案为:[
| 7 |
| 2 |
点评:本题主要考查了利用换元法求解函数的值域,解题中还有熟练应用二次函数的性质求解函数的值域

练习册系列答案
相关题目
命题“?x∈R,x2+x≥2”的否定是( )
| A、?x0∈R,x2+x≤2 |
| B、?x0∈R,x2+x<2 |
| C、?x∈R,x2+x≤2 |
| D、?x∈R,x2+x<2 |
已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),若直线y=kx与函数y=f(x)的图象恰有7个不同的公共点,则实数k的取值范围为( )
A、(2
| ||||||
B、(
| ||||||
C、(2
| ||||||
| D、(4,8) |
一个几何体的三视图如图所示,其中俯视图为正三角形,则该几何体的外接球体积为( )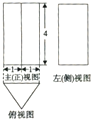

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
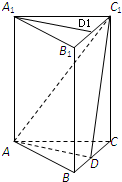 如图所示,三棱柱ABC-A1B1C1中,D为BC上一点,D1为B1C1的中点,A1B∥平面ADC1.
如图所示,三棱柱ABC-A1B1C1中,D为BC上一点,D1为B1C1的中点,A1B∥平面ADC1.