题目内容
已知A(2,1),B(2,-1),O为坐标原点,动点P(x,y)满足
=m
+n
,其中m、n∈R,且m2+n2=
,则动点P的轨迹方程是 .
| OP |
| OA |
| OB |
| 1 |
| 2 |
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:设动点P(x,y),根据向量间的关系得到x=2m+2n,y=m-n,代入m2+n2=
化简可得动点P的轨迹方程.
| 1 |
| 2 |
解答:
解:设动点P(x,y ),则
∵点P满足
=m
+n
,其中m、n∈R,
∴(x,y )=(2m+2n,m-n),
∴x=2m+2n,y=m-n,
∴m=
,n=
,
∵m2+n2=
,
∴2(
)2-(
)2=
,即
+y2=1.
故答案为:
+y2=1.
∵点P满足
| OP |
| OA |
| OB |
∴(x,y )=(2m+2n,m-n),
∴x=2m+2n,y=m-n,
∴m=
| x+2y |
| 4 |
| x-2y |
| 4 |
∵m2+n2=
| 1 |
| 2 |
∴2(
| x+2y |
| 4 |
| x-2y |
| 4 |
| 1 |
| 2 |
| x2 |
| 4 |
故答案为:
| x2 |
| 4 |
点评:本题考查了轨迹方程的求法,考查两个向量坐标形式的运算,训练了利用代入法求曲线的方程,是中档题,建立动点P(x,y )与m、n的关系是解题的关键..

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),若直线y=kx与函数y=f(x)的图象恰有7个不同的公共点,则实数k的取值范围为( )
A、(2
| ||||||
B、(
| ||||||
C、(2
| ||||||
| D、(4,8) |
一个几何体的三视图如图所示,其中俯视图为正三角形,则该几何体的外接球体积为( )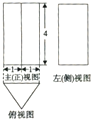

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
sin(
| ||||
tan(
|
sin(-
| ||
cos(
|
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知△ABC为等边三角形,AB=2,设点P,Q满足
=λ
,
=(1-λ)
,λ∈R,若
•
=-
,则λ=( )
| AP |
| AB |
| AQ |
| AC |
| BQ |
| CP |
| 5 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
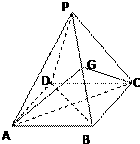 如图,四棱锥中,底面是边长为2的正方形,顶点在底面的射影是底面的中心,侧棱长为2,G是PB的中点.
如图,四棱锥中,底面是边长为2的正方形,顶点在底面的射影是底面的中心,侧棱长为2,G是PB的中点.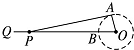 如图为曲柄连杆结构示意图,当曲柄 OA 在 OB 位置时,连杆端点 P 在 Q 的位置,当 OA 自 OB 按顺时针旋转 α 角时,P 和 Q 之间的距离为 x,已知 OA=25cm,AP=125cm,若 OA⊥AP,则 x 等于
如图为曲柄连杆结构示意图,当曲柄 OA 在 OB 位置时,连杆端点 P 在 Q 的位置,当 OA 自 OB 按顺时针旋转 α 角时,P 和 Q 之间的距离为 x,已知 OA=25cm,AP=125cm,若 OA⊥AP,则 x 等于