题目内容
已知向量
=(sinA,cosA),
=(-
,-1),
∥
,且A为锐角.
(1)求角A的大小;
(2)求函数f(x)=cos2x+4cosAsinx,(x∈R) 最大值及取最大值时x的集合.
| m |
| n |
| 3 |
| m |
| n |
(1)求角A的大小;
(2)求函数f(x)=cos2x+4cosAsinx,(x∈R) 最大值及取最大值时x的集合.
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:(1)利用向量共线定理即可得出;
(2)利用倍角公式、二次函数的单调性即可得出.
(2)利用倍角公式、二次函数的单调性即可得出.
解答:
解:(1)∵
∥
,
∴-sinA+
cosA=0,
∴tanA=
,A为锐角,
∴A=
.
(2)由(1)知cosA=
,
∴f(x)=cos2x+2sinx
=1-2sin2x+2sinx
=-2(sinx-
)2+
,
∵x∈R,∴sinx∈[-1,1],
∴当sinx=
时,f(x)有最大值
,
且x=2kπ+
或x=2kπ+
(k∈Z).
| m |
| n |
∴-sinA+
| 3 |
∴tanA=
| 3 |
∴A=
| π |
| 3 |
(2)由(1)知cosA=
| 1 |
| 2 |
∴f(x)=cos2x+2sinx
=1-2sin2x+2sinx
=-2(sinx-
| 1 |
| 2 |
| 3 |
| 2 |
∵x∈R,∴sinx∈[-1,1],
∴当sinx=
| 1 |
| 2 |
| 3 |
| 2 |
且x=2kπ+
| π |
| 6 |
| 5π |
| 6 |
点评:本题考查了向量共线定理、倍角公式、二次函数的单调性,属于基础题.

练习册系列答案
相关题目
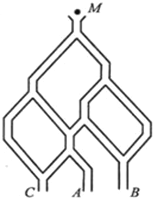 如图,一个小球从 M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
如图,一个小球从 M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.