题目内容
16.设命题p:实数x满足x2-(m+$\frac{1}{m}$)x+1<0,其中m>1.命题q:实数x,满足x2-x-6≤0.
(Ⅰ)若m=5,且p∧q为真,求实数x的取值范围;
(Ⅱ)若p是q的充分不必要条件,求实数m的取值范围.
分析 (I)对于命题p:实数x满足x2-(m+$\frac{1}{m}$)x+1<0,其中m>1,因式分解为:(x-m)$(x-\frac{1}{m})$<0,$\frac{1}{m}$<m,m=5,即可解出.
对于命题q:由x2-x-6≤0,利用一元二次不等式的解法即可得出.由于p∧q为真,则p与q都为真命题,即可得出实数x的取值范围.
(II)利用p是q的充分不必要条件,即可得出.
解答 解:(I)对于命题p:实数x满足x2-(m+$\frac{1}{m}$)x+1<0,其中m>1,因式分解为:(x-m)$(x-\frac{1}{m})$<0,解得$\frac{1}{m}<x<$m.
m=5时,可得:$\frac{1}{5}$<x<5.
对于命题q:由x2-x-6≤0,解得-2≤x≤3.
∵p∧q为真,∴$\left\{\begin{array}{l}{\frac{1}{5}<x<5}\\{-2≤x≤3}\end{array}\right.$,解得$\frac{1}{5}$<x≤3.
∴实数x的取值范围是$(\frac{1}{5},3]$.
(II)∵p是q的充分不必要条件,
∴$\left\{\begin{array}{l}{\frac{1}{5}≤\frac{1}{m}}\\{m≤3}\end{array}\right.$,又m>1,解得1<m≤3.
∴m的取值范围是(1,3].
点评 本题考查了不等式的解法、简易逻辑的判定的方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.6名同学排成一排,则甲乙恰好相邻排在一起的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{6}$ |
5.两条直线a1x+b1y+c1=0与a2x+b2y+c2=0垂直的充要条件是( )
| A. | (-$\frac{{a}_{1}}{{b}_{1}}$)(-$\frac{{a}_{2}}{{b}_{2}}$)=-1 | B. | (a1,b1)•(a2,b2)=0 | ||
| C. | -$\frac{{a}_{1}}{{b}_{1}}$=$\frac{{b}_{2}}{{a}_{2}}$ | D. | a1b2=a2b1 |
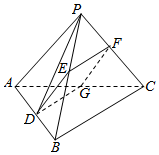 在四面体PABC中,PA=PB=PC=5,AB=BC=AC=6,点E、F、G都是所在边的中点,E、F、G这三点所确定的平面与直线AB相交于点D.
在四面体PABC中,PA=PB=PC=5,AB=BC=AC=6,点E、F、G都是所在边的中点,E、F、G这三点所确定的平面与直线AB相交于点D.