题目内容
10.已知向量$\overrightarrow{AC}$⊥$\overrightarrow{AB}$,|$\overrightarrow{AC}$|=2,则$\overrightarrow{CA}$•$\overrightarrow{BC}$的值是( )| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
分析 由$\overrightarrow{AC}$⊥$\overrightarrow{AB}$,得$\overrightarrow{AC}•\overrightarrow{AB}=0$,利用向量的减法法则把$\overrightarrow{BC}$用$\overrightarrow{AC}、\overrightarrow{AB}$表示,代入$\overrightarrow{CA}$•$\overrightarrow{BC}$并展开得答案.
解答 解:∵$\overrightarrow{AC}⊥\overrightarrow{AB}$,∴$\overrightarrow{AC}•\overrightarrow{AB}=0$,
又|$\overrightarrow{AC}$|=2,
∴$\overrightarrow{CA}•\overrightarrow{BC}=-\overrightarrow{AC}•({\overrightarrow{AC}-\overrightarrow{AB}})=-{|{\overrightarrow{AC}}|^2}+\overrightarrow{AC}•\overrightarrow{AB}$=-22+0=-4.
故选:B.
点评 本题考查平面向量的数量积运算,考查了向量的加法与减法法则,是基础题.

练习册系列答案
相关题目
20.已知函数f(x)=(x+1)ln(x+1),若函数h(x)=2f(x-1)与y=x3-mx的图象在区间[$\frac{1}{e}$,e]上有2个不同的交点.则m的取值范围是( )
| A. | [1,2] | B. | (1,2+$\frac{1}{{e}^{2}}$] | C. | (1+$\frac{1}{e}$,3) | D. | (2,4+e] |
18.已知$\overrightarrow{OA}$=(1,-2),$\overrightarrow{OB}$=(-3,1),则$\overrightarrow{AB}$=( )
| A. | (4,-3) | B. | (-4,3) | C. | (-2,-1) | D. | (2,1) |
5.两条直线a1x+b1y+c1=0与a2x+b2y+c2=0垂直的充要条件是( )
| A. | (-$\frac{{a}_{1}}{{b}_{1}}$)(-$\frac{{a}_{2}}{{b}_{2}}$)=-1 | B. | (a1,b1)•(a2,b2)=0 | ||
| C. | -$\frac{{a}_{1}}{{b}_{1}}$=$\frac{{b}_{2}}{{a}_{2}}$ | D. | a1b2=a2b1 |
2.要得到函数y=sin(x-$\frac{π}{5}$)的图象,只需将函数y=sinx的图象( )
| A. | 向左平移$\frac{π}{10}$个单位 | B. | 向右平移$\frac{π}{5}$个单位 | ||
| C. | 向左平移$\frac{π}{5}$个单位 | D. | 向右平移$\frac{π}{10}$个单位 |
19.甲、乙、丙三人站成一排站法的种数共有( )
| A. | 6 | B. | 3 | C. | 9 | D. | 12 |
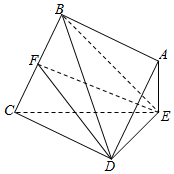 已知四棱锥E-ABCD的底面是边长为2的菱形,且AE⊥平面CDE,AE=1,CE=$\sqrt{7}$
已知四棱锥E-ABCD的底面是边长为2的菱形,且AE⊥平面CDE,AE=1,CE=$\sqrt{7}$