题目内容
10．在空间直角坐标系中，点M（-2，2，1）与点N（4，-3，1-$\sqrt{3}$）的距离是8．分析 直接利用空间两点间的距离公式求解即可．
解答 解：空间直角坐标系中，M（-2，2，1），N（4，-3，1-$\sqrt{3}$），
∴|MN|=$\sqrt{{（-2-4）}^{2}{+（2+3）}^{2}{+（1-1+\sqrt{3}）}^{2}}$=8．
故答案为：8．
点评 本题考查了空间两点间的距离公式应用问题，是基础题目．
练习册系列答案
相关题目
7．
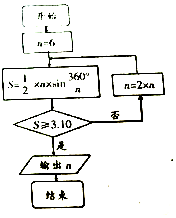如图是利用我国古代数学家刘徽的割圆术设计的程序框图，则输出的n值为（ ）
参考数据：$\sqrt{3}$≈1.732，sin15°≈0.2588，sin7.5°≈0.1305．
如图是利用我国古代数学家刘徽的割圆术设计的程序框图，则输出的n值为（ ）参考数据：$\sqrt{3}$≈1.732，sin15°≈0.2588，sin7.5°≈0.1305．
| A． | 12 | B． | 24 | C． | 48 | D． | 96 |
5．双曲线4y2-25x2=100的焦点坐标是（ ）
| A． | （-5，0），（5，0） | B． | （0，-5），（0，5） | C． | $（-\sqrt{29}，0）$，$（\sqrt{29}，0）$ | D． | $（0，-\sqrt{29}）$，$（0，\sqrt{29}）$ |
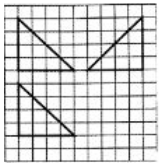如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，若该几何体的各个顶点在某一个球面上，则该球面的表面积为48π．