题目内容
设f(x)=|x-3|+|x-4|.若存在实数x满足f(x)≤ax-1则实数a的取值范围是 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由题意可得,直线y=ax-1至少有一部分在函数f(x)的图象的上方,数形结合求得实数a的取值范围.
解答:
 解:f(x)=|x-3|+|x-4|=
解:f(x)=|x-3|+|x-4|=
.
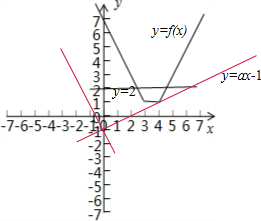
直线y=ax-1的图象是经过点(0,-1)的直线,
由题意可得,此直线至少有一部分在函数f(x)的图象的上方,
由图象可得,两条红线的斜率分别为
=
、-2,
故直线的斜率a满足a≥
,或a<-2,
故答案为:(-∞,-2)∪[
,+∞).
 解:f(x)=|x-3|+|x-4|=
解:f(x)=|x-3|+|x-4|=
|
直线y=ax-1的图象是经过点(0,-1)的直线,
由题意可得,此直线至少有一部分在函数f(x)的图象的上方,
由图象可得,两条红线的斜率分别为
| 1-(-1) |
| 4-0 |
| 1 |
| 2 |
故直线的斜率a满足a≥
| 1 |
| 2 |
故答案为:(-∞,-2)∪[
| 1 |
| 2 |
点评:本题考查绝对值不等式的解法,数形结合的应用,考查分析问题解决问题的能力,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
函数f(x)=
的定义域为( )
| (x+2)2 | ||
|
| A、{x|x>0} |
| B、{x|x<0} |
| C、{x|x>0,x≠1} |
| D、{x|x<0.x≠-2} |
已知x>0,若x+
的值最小,则x为( )
| 81 |
| x |
| A、81 | B、9 | C、3 | D、16 |