题目内容
已知向量
=(2,1),
=(1,-2),则
与
的夹角大小为( )
| a |
| b |
| a |
| b |
| A、0° | B、45° |
| C、90° | D、180° |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:根据两非零向量的数量积为0,两向量互相垂直,得出这两个向量的夹角是多少.
解答:
解:∵向量
=(2,1),
=(1,-2),
∴
•
=2×1+1×(-2)=0,
∴
⊥
=0,
∴
与
的夹角为90°.
故选:C.
| a |
| b |
∴
| a |
| b |
∴
| a |
| b |
∴
| a |
| b |
故选:C.
点评:本题考查了平面向量的应用问题,解题时应用平面向量的数量积求向量的夹角,是基础题.

练习册系列答案
相关题目
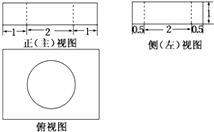
正方体P-ABC的内切球和外接球的半径之比为( )
A、
| ||
B、
| ||
C、2:
| ||
D、
|
若{an}是等比数列,若a1=1,S6=4S3,则a4=( )
| A、0 | B、1 | C、2 | D、3 |
直线x-y+2=0的倾斜角为( )
| A、60° | B、120° |
| C、45° | D、135° |
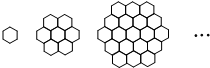 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(10)=
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(10)=