题目内容
8.设曲线x=$\sqrt{2y-{y}^{2}}$上的点到直线x-y-2=0的距离的最大值为a,最小值为b,则a-b的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$+1 | D. | 2 |
分析 利用点到直线的距离公式求出圆心到直线的距离d,由d-r求出最小值,最大值为(0,2)到直线的距离,确定出a与b的值,即可求出a-b的值.
解答 解:将x=$\sqrt{2y-{y}^{2}}$化为:x2+(y-1)2=1,
∴圆心(0,1),半径r=1,
∵圆心到直线x-y-2=0的距离d=$\frac{3\sqrt{2}}{2}$,
∴圆上的点到直线的最小距离b=$\frac{3\sqrt{2}}{2}$-1,
最大值为(0,2)到直线的距离,即a=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$
则a-b=$\frac{\sqrt{2}}{2}$+1.
故选C.
点评 此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,属于中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
3.已知某品种的幼苗每株成活率为p,则栽种3株这种幼苗恰好成活2株的概率为( )
| A. | p2 | B. | p2(1-p) | C. | ${C}_{3}^{2}$p2 | D. | ${C}_{3}^{2}$p2(1-p) |
17.若椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$过抛物线y2=8x的焦点,且与双曲线${x^2}-\frac{y^2}{2}=1$有相同的焦点,则该椭圆的方程是( )
| A. | $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ | B. | $\frac{x^2}{4}+{y^2}=1$ | C. | ${x^2}+\frac{y^2}{4}=1$ | D. | $\frac{{x}^{2}}{2}$+$\frac{y^2}{4}$=1 |
18.若函数f(x)=mx2+4mx+3>0在R上恒成立,则实数m的取值范围是( )
| A. | [0,$\frac{2}{3}$) | B. | [0,$\frac{3}{4}$) | C. | ($\frac{3}{4}$,+∞) | D. | (0,$\frac{2}{3}$) |
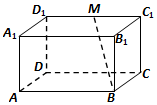 如图,在长方体ABCD-A1B1C1D1中,AB=2AD=4,A A1=2$\sqrt{2}$,M是C1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=2AD=4,A A1=2$\sqrt{2}$,M是C1D1的中点. 2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下:
2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下: