题目内容
11.已知样本数据3,2,1,a的平均数为2,则样本的标准差是( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
分析 先根据平均值求得a,再利用方差、标准差的定义,求得样本的标准差.
解答 解:样本数据3,2,1,a的平均数为2=$\frac{3+2+1+a}{4}$,∴a=2,
样本的方差S2=$\frac{1}{4}$[1+0+1+0]=$\frac{1}{2}$,∴标准差为$\sqrt{{S}^{2}}$=$\frac{\sqrt{2}}{2}$,
故选:A.
点评 本题主要考查方差、标准差的定义,属于基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
1.程序如图,要使此程序能运算出“1+2+…+100”的结果,需将语句“i=i+1”加在( ) 

| A. | ①处 | B. | ②处 | C. | ③处 | D. | ④处 |
19.如图,已知一个八面体的各条棱长均为1,四边形ABCD 为正方形,则下列命题中的假命题是( )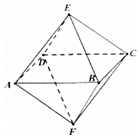

| A. | 不平行的两条棱所在的直线所成的角是60o或90o | |
| B. | 四边形AECF是正方形 | |
| C. | 点A到平面BCE的距离为$\frac{\sqrt{6}}{3}$ | |
| D. | 该八面体的顶点不会在同一个球面上. |
6.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1的左、右焦点分别为F1、F2,若双曲线上存在点P,使得|PF1|=3|PF2|,则此双曲线的离心率的取值范围是( )
| A. | (1,3] | B. | [3,+∞) | C. | (1,2] | D. | [2,+∞) |
3.函数f(x)=$\sqrt{4-|x|}$+ln$\frac{{x}^{2}-7x+12}{x-4}$的定义域为( )
| A. | (-4,3) | B. | (-4,3] | C. | (3,4] | D. | (3,4) |
20.设Sn是等差数列{an}的前n项和,且S5<S6=S7>S8,则下列结论错误的是( )
| A. | d<0 | B. | a7=0 | ||
| C. | S${\;}_{{9}_{\;}}$>S5 | D. | S6和S7均为Sn的最大值 |
 如图,圆O1和圆O2的半径都是1,|O1O2|=4,过动点P分别作圆O1和圆O2的切线PM、PN(M、N为切点),使得|PM|=$\sqrt{2}$|PN|,试建立适当平面直角坐标系,求动点P的轨迹方程.
如图,圆O1和圆O2的半径都是1,|O1O2|=4,过动点P分别作圆O1和圆O2的切线PM、PN(M、N为切点),使得|PM|=$\sqrt{2}$|PN|,试建立适当平面直角坐标系,求动点P的轨迹方程.