题目内容
16. 如图,圆O1和圆O2的半径都是1,|O1O2|=4,过动点P分别作圆O1和圆O2的切线PM、PN(M、N为切点),使得|PM|=$\sqrt{2}$|PN|,试建立适当平面直角坐标系,求动点P的轨迹方程.
如图,圆O1和圆O2的半径都是1,|O1O2|=4,过动点P分别作圆O1和圆O2的切线PM、PN(M、N为切点),使得|PM|=$\sqrt{2}$|PN|,试建立适当平面直角坐标系,求动点P的轨迹方程.
分析 建立直角坐标系,设P点坐标,列方程,化简,即可得到结果.
解答  解:以O1O2的中点O为原点,O1O2所在的直线为x轴,建立平面直角坐标系,则O1(-2,0),O2(2,0),
解:以O1O2的中点O为原点,O1O2所在的直线为x轴,建立平面直角坐标系,则O1(-2,0),O2(2,0),
由已知|PM|=$\sqrt{2}$|PN|,得PM2=2PN2.
因为两圆的半径均为1,所以PO12-1=2(PO22-1).
设P(x,y),则(x+2)2+y2-1=2[(x-2)2+y2-1],
即(x-6)2+y2=33,
所以所求轨迹方程为(x-6)2+y2=33.
点评 本题是典型的求轨迹方程的方法.考查学生的计算能力,是中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
6.一个底面为正方形的棱锥的三视图如图所示,则它的外接球的表面积为( )
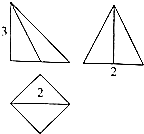

| A. | $\frac{13π}{4}$ | B. | $\frac{{\sqrt{13}π}}{2}$ | C. | 13π | D. | $\sqrt{13}π$ |
4.集合A={x|x2-5x+4<0},B={x||a-x|<1},则“B⊆A”是“a∈(2,3)”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.已知样本数据3,2,1,a的平均数为2,则样本的标准差是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
8.设集合M={x|x2-2x>0},集合N={0,1,2,3,4},则(∁RM)∩N等于( )
| A. | {4} | B. | {3,4} | C. | {0,1,2} | D. | {0,1,2,3,4} |
5.已知集合A={x|log2x<4},集合B={x||x|≤2},则A∩B=( )
| A. | (0,2] | B. | [0,2] | C. | [-2,2] | D. | (-2,2) |