题目内容
19．如图，已知一个八面体的各条棱长均为1，四边形ABCD 为正方形，则下列命题中的假命题是（ ）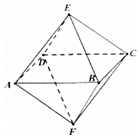
| A． | 不平行的两条棱所在的直线所成的角是60o或90o | |
| B． | 四边形AECF是正方形 | |
| C． | 点A到平面BCE的距离为$\frac{\sqrt{6}}{3}$ | |
| D． | 该八面体的顶点不会在同一个球面上． |
分析 对4个命题分别进行判断，即可得出结论．
解答 解：因为八面体的各条棱长均为1，四边形ABCD为正方形，
所以在四棱锥E-ABCD中，相邻两条侧棱所成的角为60°，而像AE与CE所成的角为90°，A正确
因为AE=CE=1，AC=$\sqrt{2}$，满足勾股定理的逆定理，所以AE⊥CE，同理AF⊥CF，AE⊥AF，所以四边形AECF是正方形；故B正确；
设点A到平面BCE的距离h，由VE-ABCD=2VA-BCE，
所以$\frac{1}{3}×1×1×\frac{\sqrt{2}}{2}=2×\frac{1}{3}×\frac{\sqrt{3}}{4}h$，解得h=$\frac{\sqrt{6}}{3}$；
所以点A到平面BCE的距离$\frac{\sqrt{6}}{3}$；故C正确；
该八面体的顶点会在同一个球面上，球心为ABCD的中心，故不正确．
故选：D．
点评 本题考查了立体几何中线线关系以及线面关系，利用了等积法求点到平面的距离．
练习册系列答案
相关题目
9．设a=log${\;}_{\frac{1}{3}}}$2，b=20.6，c=log43，则a，b，c的大小关系为（ ）
| A． | a＞b＞c | B． | c＞b＞a | C． | b＞c＞a | D． | a＞c＞b |
如图，在三棱柱ABC-A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：
4．集合A={x|x2-5x+4＜0}，B={x||a-x|＜1}，则“B⊆A”是“a∈（2，3）”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
11．已知样本数据3，2，1，a的平均数为2，则样本的标准差是（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
8．设集合M={x|x2-2x＞0}，集合N={0，1，2，3，4}，则（∁RM）∩N等于（ ）
| A． | {4} | B． | {3，4} | C． | {0，1，2} | D． | {0，1，2，3，4} |