题目内容
2.已知ax≤xlnx-x+1对任意x∈[$\frac{1}{2}$,2],恒成立,则a的最大值为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由题意ax≤xlnx-x+1对任意x∈[$\frac{1}{2}$,2]恒成立转化为a≤$\frac{xlnx-x+1}{x}$在[$\frac{1}{2}$,2]上恒成立即可;
解答 解:由题意ax≤xlnx-x+1对任意x∈[$\frac{1}{2}$,2]恒成立即a≤$\frac{xlnx-x+1}{x}$在[$\frac{1}{2}$,2]上恒成立,
令h(x)=$\frac{xlnx-x+1}{x}$=lnx+$\frac{1}{x}$-1;
h'(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$,令h'(x)=0解得x=1;
当x∈[$\frac{1}{2}$,1]时,h'(x)<0,h(x)为单调减函数;
当x∈[1,2]时,h'(x)>0,h(x)为单调增函数;
所以h(x)的最小值为h(1)=0
所以,a的最大值为0;
故选:A.
点评 本题主要考查了函数转化思想,函数求值以及导函数与原函数的关系,属中等题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
12.{an}是各项均为正数的等差数列,{bn}是等比数列,已知$\frac{a_1}{b_1}$=$\frac{a_2}{b_2}$=1,$\frac{a_3}{b_3}$=$\frac{8}{9}$,那么$\frac{a_4}{b_4}$=( )
| A. | $\frac{20}{27}$ | B. | $\frac{16}{27}$ | C. | $\frac{4}{9}$ | D. | $\frac{20}{27}$或$\frac{16}{27}$ |
17.某商场经营一批进价是30元/台的小商品,在市场试验中发现,此商品的销售单价x(x取整数)元与日销售量y台之间有如表关系:
(1)画出散点图,并判断y与x是否具有线性相关关系?
(2)求日销售量y对销售单价x的线性回归方程;
(3)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.($\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n(\overline{x})^{2}}$)
| x | 35 | 40 | 45 | 50 |
| y | 56 | 41 | 28 | 11 |
(2)求日销售量y对销售单价x的线性回归方程;
(3)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.($\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n(\overline{x})^{2}}$)
11.已知样本数据3,2,1,a的平均数为2,则样本的标准差是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
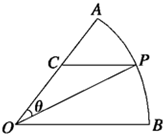 公园里有一扇形湖面,管理部门打算在湖中建一三角形观景平台,希望面积与周长都最大.如图所示扇形AOB,圆心角AOB的大小等于$\frac{π}{3}$,半径为2百米,在半径OA上取一点C,过点C作平行于OB的直线交弧AB于点P.设∠COP=θ;
公园里有一扇形湖面,管理部门打算在湖中建一三角形观景平台,希望面积与周长都最大.如图所示扇形AOB,圆心角AOB的大小等于$\frac{π}{3}$,半径为2百米,在半径OA上取一点C,过点C作平行于OB的直线交弧AB于点P.设∠COP=θ; 如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:
如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证: