题目内容
3.函数f(x)=$\sqrt{4-|x|}$+ln$\frac{{x}^{2}-7x+12}{x-4}$的定义域为( )| A. | (-4,3) | B. | (-4,3] | C. | (3,4] | D. | (3,4) |
分析 根据二次根式的性质以及对数函数的性质得到关于x的不等式组,解出即可.
解答 解:由题意得:
$\left\{\begin{array}{l}{4-|x|≥0}\\{\frac{{x}^{2}-7x+12}{x-4}>0}\end{array}\right.$,
解得:3<x<4,
故选:D.
点评 本题考查了求函数的定义域问题,考查二次根式而二次函数的性质,是一道基础题.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
11.已知样本数据3,2,1,a的平均数为2,则样本的标准差是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
8.设集合M={x|x2-2x>0},集合N={0,1,2,3,4},则(∁RM)∩N等于( )
| A. | {4} | B. | {3,4} | C. | {0,1,2} | D. | {0,1,2,3,4} |
15.定义在R上的函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,则下列不等式一定成立的是( )
| A. | f( cos$\frac{2π}{3}$)>f(sin$\frac{2π}{3}$) | B. | f(sin 1)<f(cos 1) | ||
| C. | f(sin$\frac{π}{6}$)<f(cos$\frac{π}{6}$) | D. | f(cos 2)>f(sin 2) |
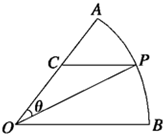 公园里有一扇形湖面,管理部门打算在湖中建一三角形观景平台,希望面积与周长都最大.如图所示扇形AOB,圆心角AOB的大小等于$\frac{π}{3}$,半径为2百米,在半径OA上取一点C,过点C作平行于OB的直线交弧AB于点P.设∠COP=θ;
公园里有一扇形湖面,管理部门打算在湖中建一三角形观景平台,希望面积与周长都最大.如图所示扇形AOB,圆心角AOB的大小等于$\frac{π}{3}$,半径为2百米,在半径OA上取一点C,过点C作平行于OB的直线交弧AB于点P.设∠COP=θ; 如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:
如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证: