题目内容
6.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1的左、右焦点分别为F1、F2,若双曲线上存在点P,使得|PF1|=3|PF2|,则此双曲线的离心率的取值范围是( )| A. | (1,3] | B. | [3,+∞) | C. | (1,2] | D. | [2,+∞) |
分析 由双曲线的定义可得|PF1|-|PF2|=2|PF2|=2a,再根据点P在双曲线的右支上,可得|PF2|≥c-a,从而求得此双曲线的离心率e的取值范围.
解答 解:∵|PF1|=3|PF2|,
∴由双曲线的定义可得|PF1|-|PF2|=2|PF2|=2a,
∴|PF2|=a,
∵点P在双曲线的右支上,
∴|PF2|≥c-a,
∴a≥c-a,即2a≥c,
∴e=$\frac{c}{a}$≤2,
∵e>1,
∴1<e≤2,
∴双曲线的离心率e的取值范围为(1,2].
故选:C.
点评 本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
16.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{5}$,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
17.某商场经营一批进价是30元/台的小商品,在市场试验中发现,此商品的销售单价x(x取整数)元与日销售量y台之间有如表关系:
(1)画出散点图,并判断y与x是否具有线性相关关系?
(2)求日销售量y对销售单价x的线性回归方程;
(3)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.($\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n(\overline{x})^{2}}$)
| x | 35 | 40 | 45 | 50 |
| y | 56 | 41 | 28 | 11 |
(2)求日销售量y对销售单价x的线性回归方程;
(3)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.($\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n(\overline{x})^{2}}$)
11.已知样本数据3,2,1,a的平均数为2,则样本的标准差是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
15.定义在R上的函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,则下列不等式一定成立的是( )
| A. | f( cos$\frac{2π}{3}$)>f(sin$\frac{2π}{3}$) | B. | f(sin 1)<f(cos 1) | ||
| C. | f(sin$\frac{π}{6}$)<f(cos$\frac{π}{6}$) | D. | f(cos 2)>f(sin 2) |
16.已知数列a1,a2,a3,a4满足a1=a4,$\frac{1}{2}$an-$\frac{1}{2{a}_{n+1}}$=an+1-$\frac{1}{{a}_{n}}$(n=1,2,3),则a1所有可能的值构成的集合为( )
| A. | {±$\frac{1}{2}$,±1} | B. | {±1,±2} | C. | {±$\frac{1}{2}$,±2} | D. | {±$\frac{1}{2}$,±1,±2} |
 如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:
如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证: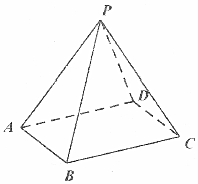 在底面是菱形的四棱锥P-ABCD中,∠BAD=60°,AB=2,PA=PC=2,PB=PD=$\sqrt{2}$.
在底面是菱形的四棱锥P-ABCD中,∠BAD=60°,AB=2,PA=PC=2,PB=PD=$\sqrt{2}$.