题目内容
18.已知等比数列{an}的公比为正数,且4a2a8=a42,a2=1,则a6=( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | $\frac{1}{64}$ |
分析 由题意和等比数列的性质可得q,再由等比数列的通项公式可得.
解答 解:∵等比数列{an}的公比q为正数,
由4a2a8=a42和a2=1可得4a52=a42,
∴q2=$\frac{{{a}_{5}}^{2}}{{{a}_{4}}^{2}}$=$\frac{1}{4}$,解得q=$\frac{1}{2}$,
∴a6=a2q4=1×($\frac{1}{2}$)4=$\frac{1}{16}$,
故选:B.
点评 本题考查等比数列的通项公式,求出数列的公比是解决问题的关键,属基础题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
9.已知集合A={x|-1≤x≤1},B={x|x2-5x+6≥0},则下列结论中正确的是( )
| A. | A∩B=B | B. | A∪B=A | C. | A?B | D. | ∁RA=B |
13.sin10°cos50°+cos10°sin50°的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
10.下列表格所示的五个散点,原本数据完整,且利用最小二乘法求得这五个散点的线性回归直线方程为$\widehaty$=0.8x-155,后因某未知原因第5组数据的y值模糊不清,此位置数据记为m(如表所示),则利用回归方程可求得实数m的值为( )
| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |
| A. | 8.3 | B. | 8.2 | C. | 8.1 | D. | 8 |
7. 如图是高二数学选修1-2第二章“推理与证明”的知识结构图,已知反证法是一种间接证明方法,如果要在图中加入反证法,则应把它放在( )
如图是高二数学选修1-2第二章“推理与证明”的知识结构图,已知反证法是一种间接证明方法,如果要在图中加入反证法,则应把它放在( )
 如图是高二数学选修1-2第二章“推理与证明”的知识结构图,已知反证法是一种间接证明方法,如果要在图中加入反证法,则应把它放在( )
如图是高二数学选修1-2第二章“推理与证明”的知识结构图,已知反证法是一种间接证明方法,如果要在图中加入反证法,则应把它放在( )| A. | “合情推理”的下位 | B. | “演绎推理”的下位 | ||
| C. | “直接证明”的下位 | D. | “间接证明”的下位 |
8.若数列{an}通项为an=kn,则“数列{an}为递增数列”的一个必要不充分条件是( )
| A. | k≥0 | B. | k>1 | C. | k>0 | D. | k<0 |
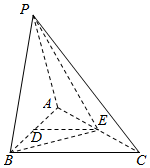 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.