题目内容
6.若变量x,y满足约束条件$\left\{\begin{array}{l}4x+3y≤12\\ x≥0\\ y≥0\end{array}$,则z=$\frac{y+3}{x+1}$的取值范围是[$\frac{3}{4}$,7].分析 作出不等式组对应的平面区域,利用z的几何意义结合直线的斜率公式进行求解即可.
解答 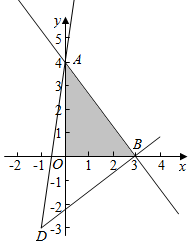 解:作出不等式组对应的平面区域,
解:作出不等式组对应的平面区域,
z=$\frac{y+3}{x+1}$的几何意义是区域内的点到定点(-1,-3)的斜率,
由图象知DA的斜率最大,DB的斜率最小,
∵A(0,4),B(3,0),
∴z的最大值为z=$\frac{4+3}{1}=7$,z的最小值为z=$\frac{0+3}{3+1}$=$\frac{3}{4}$,
即,z=$\frac{y+3}{x+1}$的取值范围是[$\frac{3}{4}$,7],
故答案为:[$\frac{3}{4}$,7].
点评 本题主要考查线性规划的应用,利用直线斜率的几何意义以及数形结合是解决本题的关键.

练习册系列答案
相关题目
14.由曲线y=$\sqrt{x}$,y=x-2及x轴所围成的封闭图形的面积是( )
| A. | 4 | B. | $\frac{10}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{15}{4}$ |
1.设全集U=R,已知集合A={-2,-1,0,1,2,3},B={x|x2+x-2≥0},则集合A∩∁UB=( )
| A. | {-1,0} | B. | {-1,0,1} | C. | {-2,-1,0,1} | D. | {-1,0,1,2} |
18.已知等比数列{an}的公比为正数,且4a2a8=a42,a2=1,则a6=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | $\frac{1}{64}$ |
15.设α、β、γ是三个不同的平面,a、b是两条不同的直线,下列四个命题中正确的是( )
| A. | 若a∥α,b∥α,则a∥b | |
| B. | 若a⊥α,b⊥β,a⊥b,则α⊥β | |
| C. | 若a∥α,b∥β,a∥b,则α∥β | |
| D. | 若a,b在平面α内的射影互相垂直,则a⊥b |
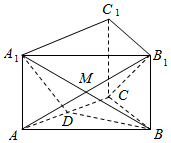 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,△ABC是边长为2的正三角形,D是AC的中点.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,△ABC是边长为2的正三角形,D是AC的中点.