题目内容
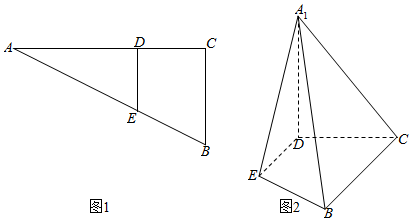
8. 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.(1)求证:AB⊥PE;
(2)求三棱锥P-BEC的体积.
分析 (1)连结PD,则由三角形三线合一可得AB⊥PD,又BC∥DE,BC⊥AB,故AB⊥DE,于是AB⊥平面PDE,得出AB⊥PE;
(2)利用等边三角形的性质计算PD和S△BCE,代入棱锥的体积公式计算.
解答  解:(1)连结PD,∵D,E分别是AB,AC的中点,
解:(1)连结PD,∵D,E分别是AB,AC的中点,
∴DE∥BC,又∠ABC=90°,
∴DE⊥AB.
又∵PA=PB,D为AB中点,∴PD⊥AB.
又PD?平面PDE,DE?平面PDE,PD∩DE=D,
∴AB⊥平面PDE,∵PE?平面PDE,
∴AB⊥PE.
(2)∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PD⊥AB,PD?平面PAB,
∴PD⊥平面ABC,
∵PA=PB=AB=2,D是AB中点,∴BD=1,PD=$\sqrt{3}$,
又∵S△BCE=$\frac{1}{2}BC•BD$=$\frac{1}{2}×3×1$=$\frac{3}{2}$.
∴VP-BCE=$\frac{1}{3}{S}_{△BCE}•PD$=$\frac{1}{3}×\frac{3}{2}×\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
18.已知等比数列{an}的公比为正数,且4a2a8=a42,a2=1,则a6=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | $\frac{1}{64}$ |