题目内容
9.已知x,y,z为正实数,则$\frac{xy+yz}{{x}^{2}+{y}^{2}+{z}^{2}}$的最大值为( )| A. | $\frac{2\sqrt{3}}{5}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
分析 根据基本不等式可得x2+$\frac{1}{2}$y2≥$\sqrt{2}$xy,z2+$\frac{1}{2}$y2≥$\sqrt{2}$yz,问题得以解决.
解答 解:x2+$\frac{1}{2}$y2≥$\sqrt{2}$xy,z2+$\frac{1}{2}$y2≥$\sqrt{2}$yz,
∴x2+y2+z2≥$\sqrt{2}$xy+$\sqrt{2}$yz=$\sqrt{2}$(xy+yz),
∴$\frac{xy+yz}{{x}^{2}+{y}^{2}+{z}^{2}}$≤$\frac{\sqrt{2}}{2}$,当且仅当x=z=$\frac{\sqrt{2}}{2}$y时取等号,
故$\frac{xy+yz}{{x}^{2}+{y}^{2}+{z}^{2}}$的最大值为$\frac{\sqrt{2}}{2}$,
故选:B
点评 本题主要考查基本不等式的应用,注意检验等号成立的条件,式子的变形是解题的关键,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知直线a,b分别在两个不同的平面α,β内.则“直线a和直线b垂直”是“平面α和平面β垂直”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图所示,则函数表达式为( )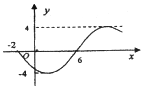

| A. | y=-4sin($\frac{π}{8}$x-$\frac{π}{4}$) | B. | y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$) | C. | y=4sin($\frac{π}{8}$x-$\frac{π}{4}$) | D. | y=4sin($\frac{π}{8}$x+$\frac{π}{4}$) |
 如果执行右边的程序框图,输出的值为x,则${x}^{\frac{1}{2}}$+log3x=5.
如果执行右边的程序框图,输出的值为x,则${x}^{\frac{1}{2}}$+log3x=5.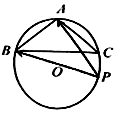 如图,在△A BC中,三内角 A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,$a=\sqrt{3}$,S为△A BC的面积,圆 O是△A BC的外接圆,P是圆 O上一动点,
如图,在△A BC中,三内角 A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,$a=\sqrt{3}$,S为△A BC的面积,圆 O是△A BC的外接圆,P是圆 O上一动点,